バックナンバーはこちら。
https://www.simulationroom999.com/blog/stock-predict-matlabpython-backnumber/
はじめに
前回は、極大値、極小値の求め方について解説。
- 極大値は、「微分値がプラス→0→マイナス」となるところ。
- 極小値は、「微分値がマイナス→0→プラス」となるところ。
になる。
プログラム的には以下を行う。
- 極大値を探す場合は差分の結果マイナス。
- 極小値を探す場合は差分の結果プラス。
今回はこれをMATLABで書くとどうなるかを見て行く。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
極大値と極小値の特定する(MATLAB版)

で、今回から極大値、極小値をプログラム的に求めるんだよね?
とりあえずMATLABからやるのかな?

そうだね。
さっそくコードを見せよう。
N=512;
x=linspace(-pi,pi,N);
fx=sin(x)+sin(3*x)+sin(5*x);
ft=fx;
hold on
max_fx=max(fx);
max_ft=max(ft);
plot(fx);
% 極大値、極小値特定
maxima = zeros(1,N);
minima = zeros(1,N);
fxTmp=fx(1);
mode = 0;
for i = 2:N
if mode == 0
if fx(i)>fxTmp
minima(i)=ft(i)*(max_fx/max_ft);
mode = 1;
end
fxTmp=fx(i);
end
if mode == 1
if fx(i)<fxTmp
maxima(i)=ft(i)*(max_fx/max_ft);
mode = 0;
end
fxTmp=fx(i);
end
end
maxima(maxima==0)=NaN; % 極大値だけを残す
minima(minima==0)=NaN; % 極小値だけを残す
plot(maxima,'ro') % 極大値をplot
plot(minima,'bo') % 極小値をplot
実行結果

上記コードの実行結果は以下だ。
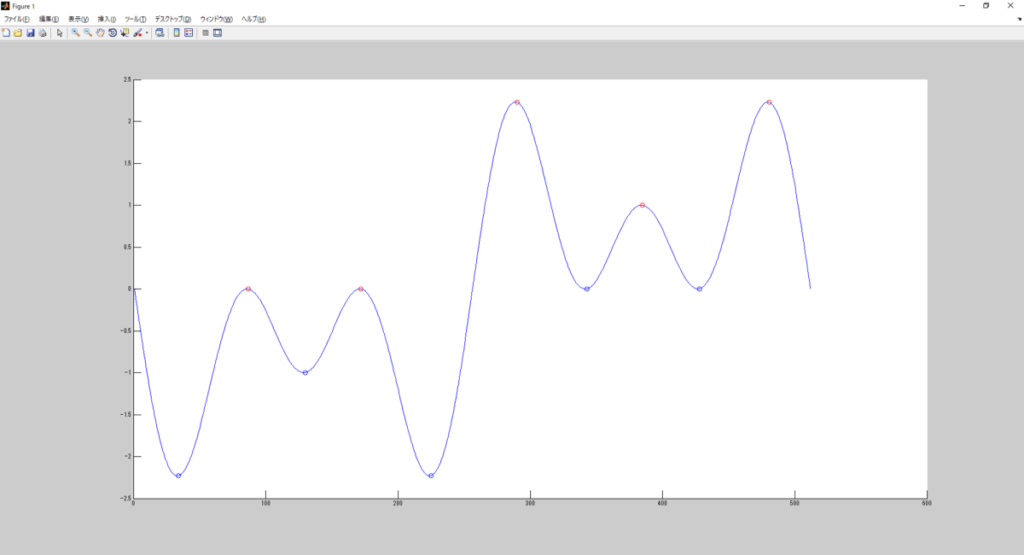

あ、極大値に赤丸、極小値に青丸を置いてるのね。

極大値、極小値の特定自体は前回言ってた通り、
- 極大値を探す場合は差分の結果マイナス。
- 極小値を探す場合は差分の結果プラス。
をやってるってことか。
今回のコードの問題点

今回のコードは一部問題点があって、
最初に極小値が来ることを想定しているところにある。

え?
それでいいの?

本当の極大値、極小値を求める際は、この点も加味する必要はあるのだが、
今回は欲しいのは買付、売却のタイミングを知りたいだけなんで、これでもOKとしようと思う。

ちなみに最初に来るのが極小値じゃなくて極大値の場合、どういう動きになるの?

最初の点が極小値になるだけだな。
試しに実験波形を反転させたものを入力してみよう。
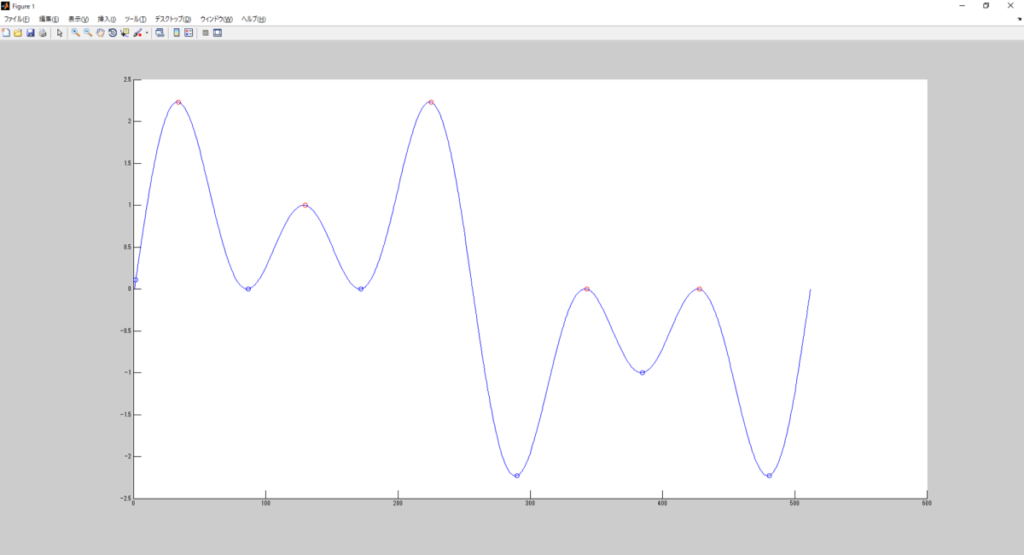

なるほど。
少なくとも先に買付が来るという意味では辻褄合うのか。

そうそう。
だから、今回の使い方に於いてはむしろ都合が良いとも言える。
まとめ

まとめだよ。
- 極大値と極小値の特定のMATLABコードを作成。
- 上記コードの動作確認。
- 極大値に赤丸、極小値に青丸を置いてる。
- 一部問題点あり。
- 最初に極小値が来ることを想定している。
- しかし、最初に買付をする想定なので、むしろ今回のコードの方が都合が良い。
バックナンバーはこちら。




コメント