バックナンバーはこちら。
https://www.simulationroom999.com/blog/stock-predict-matlabpython-backnumber/
はじめに
前回はMATLABによるベクトルローテーションとしてcircshift関数の挙動実験を行った。
基本は列ベクトルに対して行うもので行ベクトルだと期待する動作はしなかったが、
引数の設定次第では行ベクトルに対してもローテーション可能。
基本は列ベクトルにしておいた方が良さそうである。
今回は実際に、FFT出力の周波数分布をローテーションさせてみる。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
FFT出力の周波数分布をローテーション

circshift関数でローテーションできるのはわかったから、
早速MATLABでFFT出力をローテーションさせてみよう。

ざっと書いたコードがこれだ。
N=1024;
L=pi;
x=linspace(-L,L,N)';
k=-N/2:N/2-1;
ft=sin(x)+sin(3*x)+sin(7*x);
% 変換前波形
subplot(2,1,1)
plot(x,ft)
title('f(t)');
grid();
% FFT後にローテーション
Fw=fft(ft);
Fw_tmp=circshift(Fw,N/2);
subplot(2,1,2);
mask = (-10<=k & k<=10);
plot(k(mask),abs(Fw_tmp(mask)));
title('F(\omega)');
grid();出力結果

そして結果がこれ。
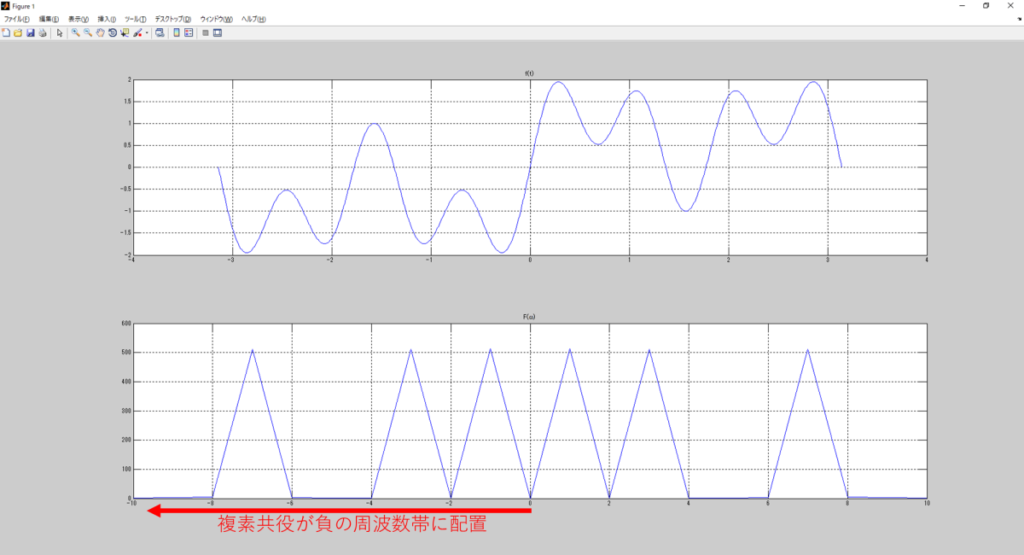

ちゃんと対象に配置されて、
1[Hz]、-1[Hz]
3[Hz]、-3[Hz]
7[Hz]、-7[Hz]
になったね。

あまりよく理解できてないのだけど、
これでバンドパスフィルタがやり易い分布になったってことで良いのかな?

その話はPython側の対応をしたあとに改めてする予定だが、
正と負の違いだけで同様の配置になってるので、割と処理し易い形にはなってる。
まぁ以前もいったが必須の処理ではなく、確認のし易さ、処理のし易さ重視の配置ってことだな。

実際に処理をする時にどうするかを見てみるしかなさそうかー。

そうね。
それが手っ取り早いね。

じゃー、次はPythonで同じことができるかってことか。
まとめ

まとめだよ。
- FFT出力の周波数分布をローテーションをMATLABで実施。
- 複素共役が0点を中心とした線対称になるように配置。
- この配置の方が確認し易さ、処理のし易さが増す想定。
- よって、配置が意識できていればやらなくてもOK。
- 効能は実際の処理をする際に確認。
バックナンバーはこちら。




コメント