【FFT】MATLAB、Pythonで株価予測 その25【IFFT④】

バックナンバーはこちら。
https://www.simulationroom999.com/blog/stock-predict-matlabpython-backnumber/

はじめに
登場人物
FFTにとっての周波数
Pythonコード
結果確認
使ってる数式
まとめ

はじめに

前回は、sin波のサンプリング期間を伸ばした状態でFFTで周波数分布を確認。
元々のサンプリング期間が2πだったものに対し、
4πになりsin波自体はサンプリング期間の振動数は増える。
FFTは入力サンプリング期間を1周期と見なすため、sin波は1Hzから2Hzの成分に見える。
物理的な周波数とは異なるため、注意が必要。

ここまでMATLABでやって来たので、Python側のコードも起こしてみる。

登場人物

博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1

エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1

FFTにとっての周波数

太郎くん

前回の実験で、FFTが示す周波数の意味がわかった感じだ。
入力サンプリングを1周期と見なした際の周波数。
よって、物理的な周波数とは異なる。
ってことだね。

フクさん

そうそう。

フクさん

(というか業務でFFT使ってるって言ってたけど、今までどうしてたんだろう？)

Pythonコード

太郎くん

今まではMATLABでやって来てたからそろそろPython側も同じようにできるか確認した方が良くない？
タイトル詐欺って言われるよ。

フクさん

それはいかん！

フクさん

まぁ流れは一緒だからサラッとコードを貼ってしまおう。
前回の\(-2\pi～2\pi\)の\(4\pi\)を1周期とした場合のコードだ。

import numpy as np
import matplotlib.pyplot as plt

N=1024
L=2*np.pi
x=np.linspace(-L,L,N)
k=np.arange(0,N)
ft=np.sin(x)

fig = plt.figure()

ax = fig.add_subplot(4, 1, 1)
ax.plot(x,ft)
ax.set_title('f(t)')

ax1 = fig.add_subplot(4, 1, 1)
ax1.plot(x,ft)
ax1.set_title('f(t)')

Fw=np.fft.fft(ft)

ax2 = fig.add_subplot(4, 1, 2)
ax2.plot(k,np.abs(Fw))
ax2.set_title(r'$F(\omega)$')

ax3 = fig.add_subplot(4, 1, 3)
ax3.plot(k[0:10],abs(Fw[0:10]))
ax3.set_title(r'$F(\omega)$ expansion')

fx=np.fft.ifft(Fw)

ax4 = fig.add_subplot(4, 1, 4)
ax4.plot(x,fx.real)
ax4.set_title('f(x)')

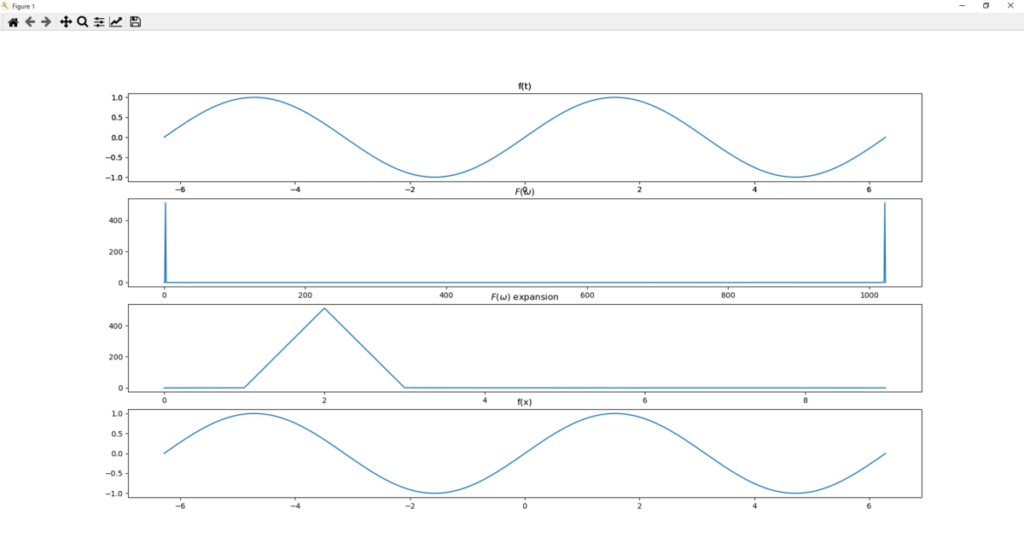
plt.show()