バックナンバーはこちら。
https://www.simulationroom999.com/blog/model-based-of-minimum-2-backnumber/
はじめに
前回、
constantForceモデルとmassモデルを組み合わせたシンプルなModelicaモデルをシミュレーションしてみた。
加速度の確認をしたがそれ以外のパラメータも確認してみる。
具体的には以下。
- 速度
- 移動距離
速度と移動距離についての関係性ついてに簡単に解説。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
他のシミュレーション結果のパラメータ

前回はmassの加速度を確認したけど、
今回は他のパラメータも確認だね。

そうだね。

といっても
見るパラメータとしては、
- 加速度
- 速度
- 移動距離
だな。

これも予測できるの?

できるよ。
前々回も話した話したかもしれないけど、
加速度を積分すれば速度。
速度を積分すれば移動距離。
なんで。

なるほど。
それほど難しい話ではなさそう。
他のシミュレーション結果のパラメータ確認

じゃ、OpenModelica Connection Editorのプロットの画面を開く。
そして、右側の変数ブラウザの
「a」、「s」、「v」にチェックを入れる。

それぞれはどういうものかというと・・・。
一応パラメータの説明が隣に載ってるから、これを見ればわかりそうだな。

「a」が加速度、「s」が位置こと移動距離、「v」が速度。
だね。

その通り。

うん。
プロットが表示された。
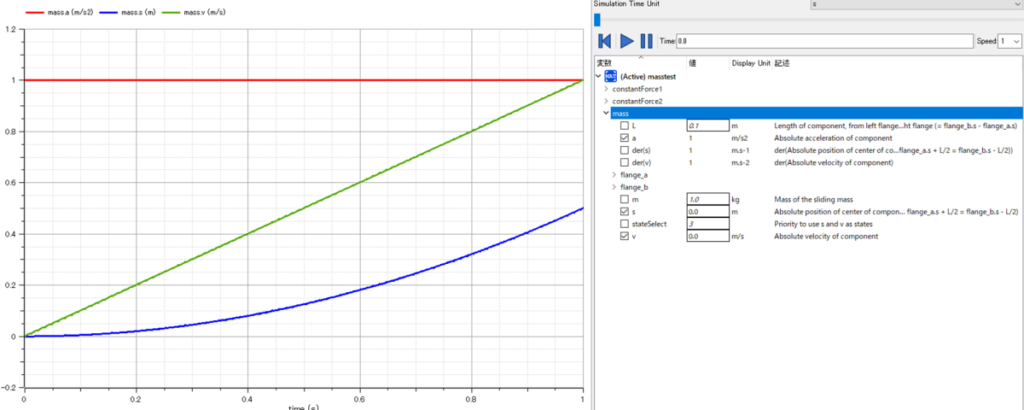

速度が\(1[m/s^2]\)固定なんで、
速度は1秒毎に\(1[m/s]\)のペースで上がり続けてるね。

移動距離は・・・どう表現したらいいんだ???

ここを見てみよう。

ここの話を元にすると・・・。

移動距離は
\(\displaystyle \vec{x}=\vec{v_0}t+\frac{1}{2}\vec{a}t^2\)
で
速度が
\(\vec{v}=\vec{v_0}+\vec{a}t\)
今回は初速度\(\vec{v_0}\)は0と見なしてOKなんで、
速度は\(\vec{v}=\vec{a}t\)と見なせる。
移動距離の式に入れると
\(\displaystyle \vec{x}=\frac{1}{2}\vec{v}t\)
か。

速度と時間をかけて2で割った値が移動距離ってことか。
シミュレーション結果とも一致してるね。

と言う感じで各モデルの内部パラメータを参照する形で
シミュレーション結果が確認できるってことになる。

Simulinkの場合はスコープとか設置してたから、
それと比べるといろいろなパラメータが細かく見れて便利な気がする。
まとめ

まとめだよ。
- 他のシミュレーション結果のパラメータを確認
- 加速度に加えて、速度と移動距離。
- OpenModelica Connection Editorのプロットの画面の変数ブラウザでチェックを入れるだけで確認可能。
- それぞれのパラメータの関係性を確認。
- 加速度を積分して速度。
- 速度を積分して移動距離。
バックナンバーはこちら。






コメント