バックナンバーはこちら。
https://www.simulationroom999.com/blog/model-based-of-minimum-2-backnumber/
はじめに
前回constantForceモデルとmassモデルを組み合わせたシンプルなModelicaモデルを作成した。
今回はこのモデルの意味合いの説明をする。
ついでにどのような動きになるか予測してみる。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
前回のモデル復習

今回は前回作ったconstantForceモデルとmassモデルの組み合わせモデルの説明をするんだよね?

そうそう。
前回のモデルを貼っておこう。
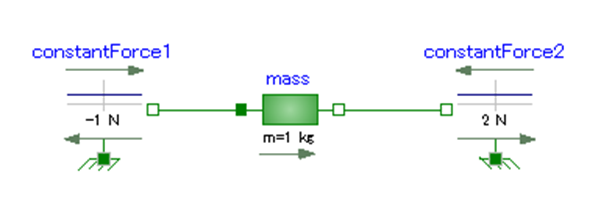
何をしているモデルなのか?

このモデル、
見た目だけでいうと真ん中のmassを引っ張り合ってるって感じなのかな?

その通り。
\(1[N]\)と\(2[N]\)で引っ張り合ってるって状態だ。

んー、でもそうなると、
左側のconstantForceが\(1[N]\)じゃなくて\(-1[N]\)になってるのが気になるなー。

あー。
クラフィックエディタ上のアイコンだと分かりにくいんだけど、
力を加える方向って必ず一方向になるんだよ。
このエディタ上の表現だと、
プラス方向は右。
マイナス方向は左。
みたいなイメージ。

あー!
なるほど。
\(-1[N]\)にしておかないと逆方向に引っ張るモデルにならないってことだね。

そうそう。
Modelica自体はそもそもプログラミング言語なんでね。
クラフィックエディタ上のアイコンと表現が一致しないことがあるんで
そこらへんは気を付ける必要はあるかな。

確かに、これは知らなかったら一生ハマりっぱなしだな・・・。
どんな結果になるか予測

動かす前にどんな動きになるか予測してみよう。

え゛

力と質量が分かってるんで、加速度が求められるよね?

…。

運動方程式で
\(\vec{F}…力\)
\(m…質量\)
\(\vec{a}…加速度\)
\(\vec{F}=m\vec{a}\)
ってあるじゃん?

あー、そっか!
力と質量が確定しているから
\(\vec{F}=m\vec{a}\)
\(\displaystyle\vec{a}=\frac{\vec{F}}{m}\)
\(\vec{F}\)と\(\vec{a}\)に値を入れれば加速度も求まる!

確かここで見た気がする。

じゃー、今回の加速度は?

massは完全剛体って以前言ってたから、
伸縮とかは考えなくて良くて、
そうすると、左右の力は単純に合成してOKで
\(2[N]+(-1[N])=1[N]\)

SI単位系での質量の単位は\(kg\)で、今回の質量は\(1[kg]\)
さっきの運動方程式に入れ込んで、
\(\displaystyle\vec{a}=\frac{\vec{F}}{m}\)
\(\displaystyle\vec{a}=\frac{1}{1}\)
\(\vec{a}=1\)
で、答えは\(1[m/s^{2}]\)だ!

正解だ。

よっしゃ!

加速度が分かれば、
それを積分して速度。
速度を積分して距離。
が分かるってことになる。

なるほど。

本当にそうなるか実際にシミュレーションして確認してみよう。
まとめ

まとめだよ。
- 前回作成したモデルが何を示しているか確認。
- massを引っ張り合ってるモデル。
- グラフィックエディタだと分かりにくいがマイナス符号を付けないと逆向きの力にはならない。
- シミュレーション結果を事前に予測してみる。
- 運動方程式を使用する。
- 質量と力が分かっているので、加速度が求められる。
- 加速度から速度、速度から距離。
バックナンバーはこちら。





コメント