https://www.simulationroom999.com/blog/derivation-of-motor-transfer-function/
はじめに
ここで言う運動方程式は回転の運動方程式となる。
(モーター自身は回転運動しかしないため。)
回転の運動方程式の導出は以下参照。
その他のモーター関連の情報はモータータグから
回転の運動方程式
以下が回転の運動方程式となる。
\(T\):トルク\([N・m]\)
\(J\):イナーシャ\([kgm^2]\)
\(θ\):移動角\([rad]\)
$$T=J\frac{d^2}{dt^2}θ$$
上記の式をラプラス変換する。
- \(sθ\)を角速度\(ω\)と置き換える。
- トルク\(T\)をロータートルク\(T_r\)と反力\(-T_L\)の和に置き換える。
\(T_r\):ロータートルク\([N・m]\)
\(T_L\):反力\([N・m]\)
\(J\):イナーシャ\([kgm^2]\)
\(ω\):角速度\([rad/s]\)
\begin{align}
T_r-T_L&=Jsω\\\\
\frac{T_r-T_L}{ω}&=Js \\\\
\frac{ω}{T_r-T_L}&=\frac{1}{J}\frac{1}{s} \\\\
\end{align}
イナーシャ\(J\)はローターの形状、質量から算出される定数。
反力\(T_L\)は仕事させたときに初めて確定する。
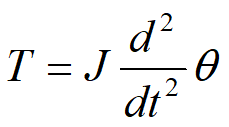






コメント