バックナンバーはこちら
https://www.simulationroom999.com/blog/model-based-of-minimum-backnumber/
はじめに
前回はプラントモデルのリアルさをちょっと追求し
それに伴うPIDの各ゲインの調整を行った。
今回は横道にそれて、ちょっとした実験を行うことにした。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
可変にする対象は?

前回、不穏なことを言ってたけど、
それの話になるのかな?

(別に不穏なことを言ったわけでは・・・。)

前回、積分単位時間という時間パラメータを調整したと思うんだけど、
もう一個、時間のパラメータがあったよね?

あー、\(Δt\)こと制御周期のこと?

今回はこれを可変にする。

え?そんなことして良いの?
制御周期って固定じゃないとまずいと思うんだけど・・・。

うん。
仕様としては周期は固定が望ましい。
しかし、折角パラメータとして存在しているので
その特性、性質を知っておくと後々便利な使い道が思いつくかもしれない。

(すごい。なんか伏線っぽいの張ってきた。)

(・・・。どうしよう。
この伏線はちゃんと回収できるのだろうか・・・。)
可変駆動周期を作る

まず駆動周期を作るため、
無理やり変動性があるクロックを生成する。

具体的にはどんな感じ?

適当な角速度の波形を作って、
それを積分して、
sin()に入れた波形をクロックにする。
以下の感じ。
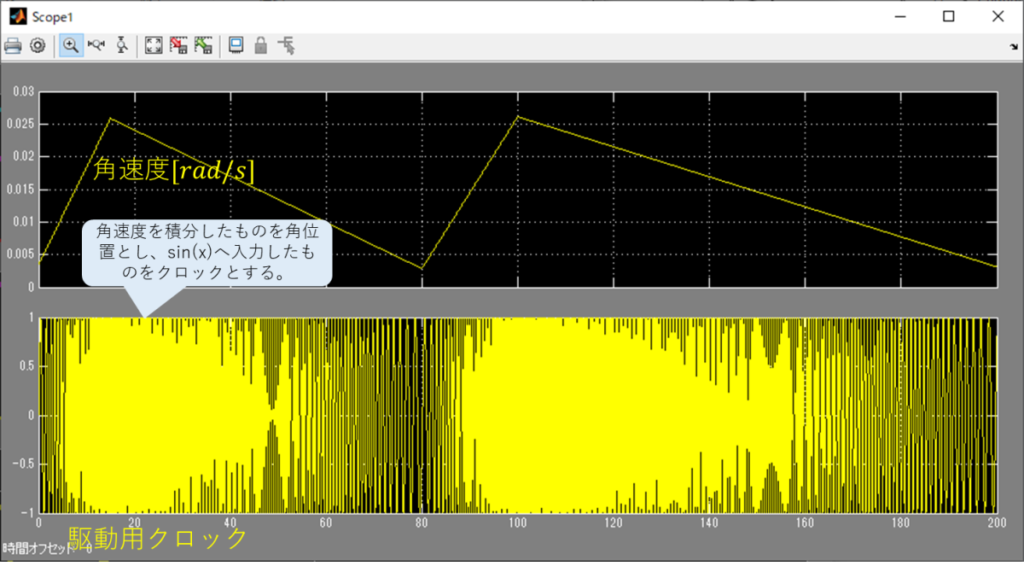

sin(x)は入力角位置\([rad]\)に依存して値が決定する。
よって、角速度\([rad/sec]\)の増減が周波数の増減となる。

細かいところはよう分らんが、
これで可変周期というものが出来たわけだ。
そのままPIDを駆動してみる。

そのまま前項のクロックでPIDを駆動させてみたのが以下。
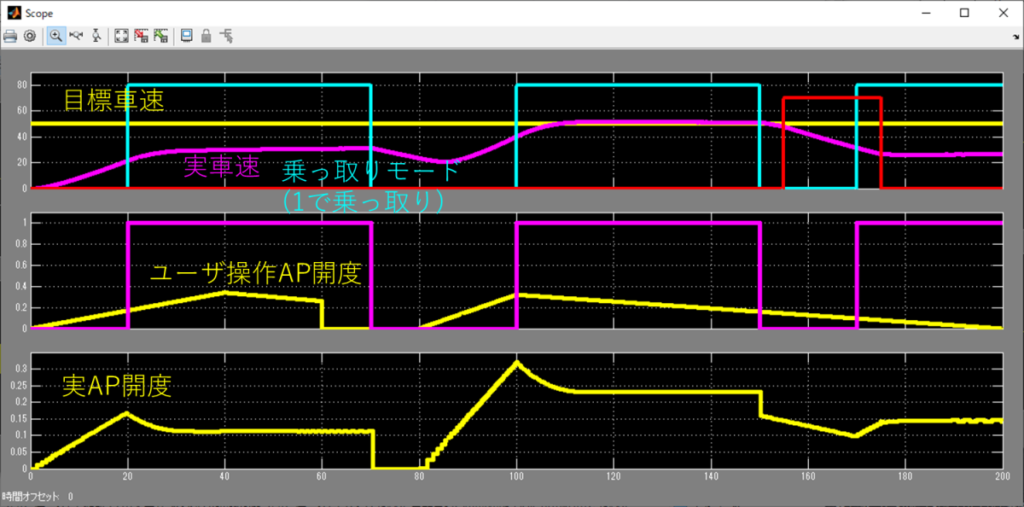

んー、なんともダメな感じだねー。

案の定と言えば案の定だが、追従しきれていない。
本来であれば、PIDの各ゲインを再調整ということになるが、
クロックが一定ではない以上、
定数というわけにもいかない。

うん。それは分かる。
PID制御器見直し

ここでPID制御器を見直してみよう。
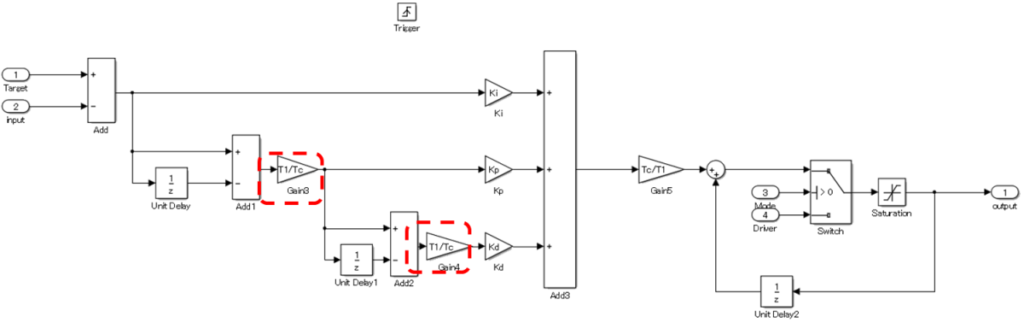

前回同様にPIDの各ゲイン以外の数学的に出てきたパラメータの、
積分単位時間\(T1\)と制御周期\(T_c\)に着目。
まさに制御周期\(T_c\)を可変にしてしまえば解決するはず。たぶん

「たぶん」って何?!
しっかりしてよ!

まぁ実は私も実際にやるのは初めてで。
でも理屈上は問題無いんで。
PID制御器修正

んで、PID制御器を修正してみた。
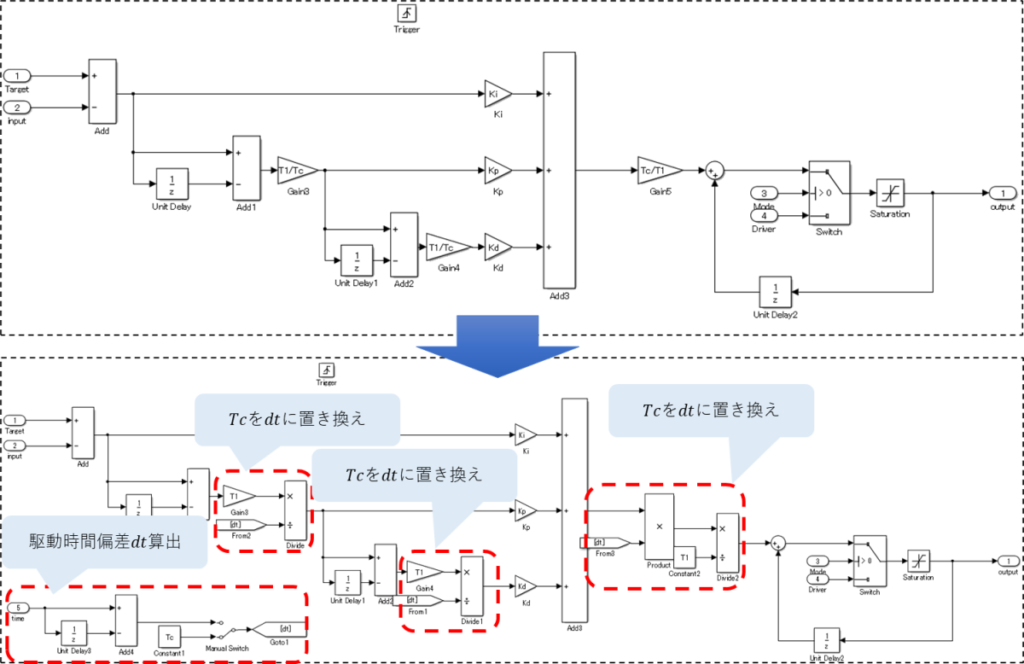

そうか。
定数から変数にしたんで、Gainブロックじゃ都合悪いんだね。
新型PID動作確認

そして、
実際に動作させたのがこちら。
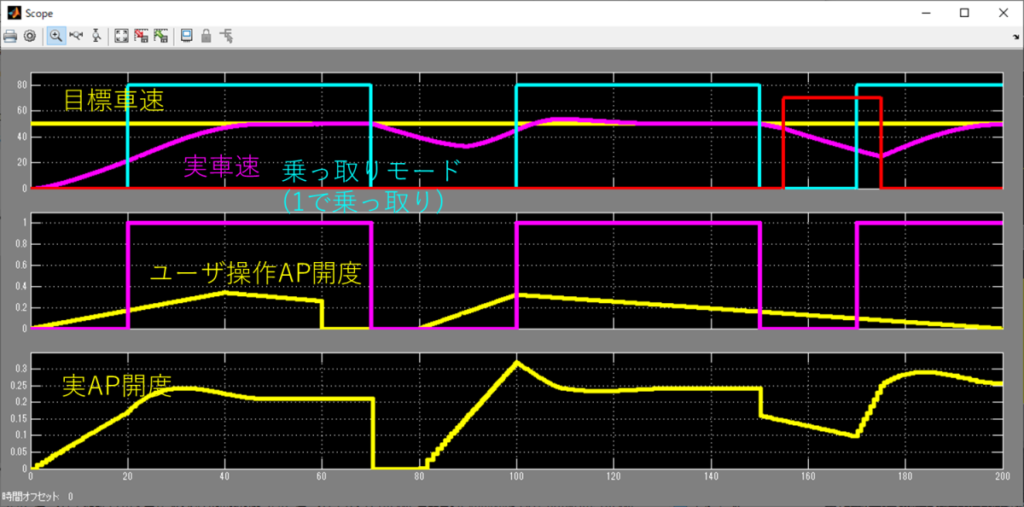

少しガタついてる部分はあるけど、
制御としては従来と変わらないね。

うん。
どうやら理屈通りうまくいったようだ。

周期を可変にした分、\(Δt\)も可変にしたんで、
数学的には同一なはずなんだ。
まぁ実際には離散化した時の誤差があるんで、
完全一致にはならないけど。

完全一致ではないだろうけど、
これはこれで十分な性能だね。
各ゲイン

\(Δt\)を可変にしたわけなんだけど、
一般的なPIDに解釈しなおすとどうなるのかな?

こうなるよ。
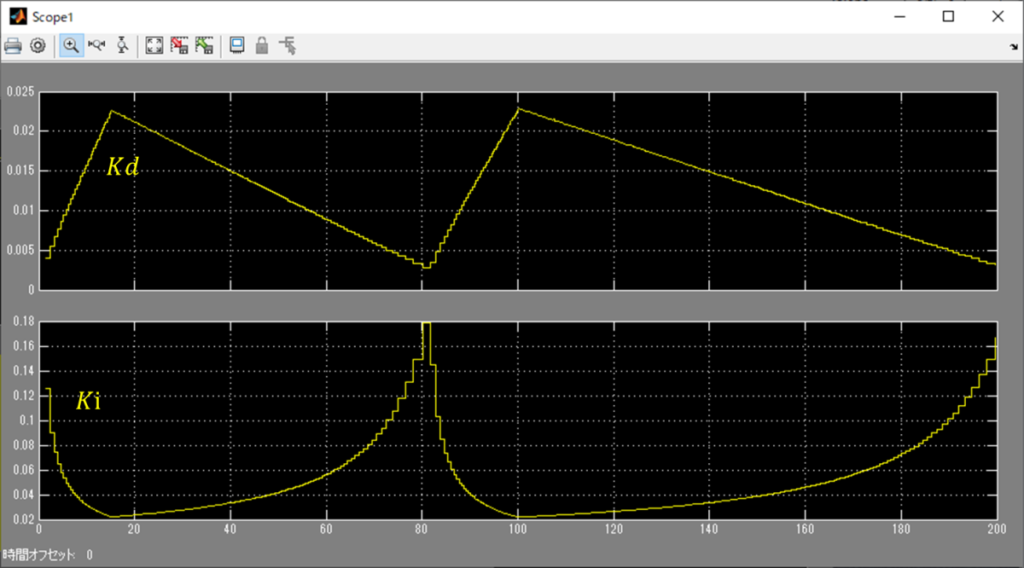

ちなみに\(K_p\)は変化しない。

\(K_d\)が角速度に比例して、
\(K_i\)が角速度に反比例する感じか。

その通り。

今回も中々楽しめた。
(あとは、伏線回収を待つばかりか)

(伏線回収どうしよう)
まとめ

まとめだよ。
- \(Δt\)をパラメータとして扱うことができる。
- これにより、PIDの駆動周期が可変でも対応可能。
- \(Δt\)と駆動周期が同時に変化するので、数学的には通常のPIDと同一と言える。
- 総和法、差分法による誤差分があるため完全一致とはいかないが、ほとんどの制御では問題なく動作する。
バックナンバーはこちら




コメント