バックナンバーはこちら
https://www.simulationroom999.com/blog/model-based-of-minimum-backnumber/
はじめに
前回、PID制御を離散化した。
Simulinkへ転記しても動作するレベルまで来たが、
制御対象が無いため、動作確認ができない。
制御対象の仕様を決めていく。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
アクセル開度と車速の関係性は?

で、制御対象ってどうしたら良いの?
車両側の振る舞いとか良く分かっていないよ?

まぁ、
完全に車両を再現する必要はないかな。

そーなの?
それだとしても、一体どうしたら良いか・・・。

世の中に存在する制御対象はおおよそ一次遅れ系で表現できる。
これを考え方を利用する。

一次遅れ系?

動作イメージはこんな感じ。
青点線が入力として、黒線が出力。
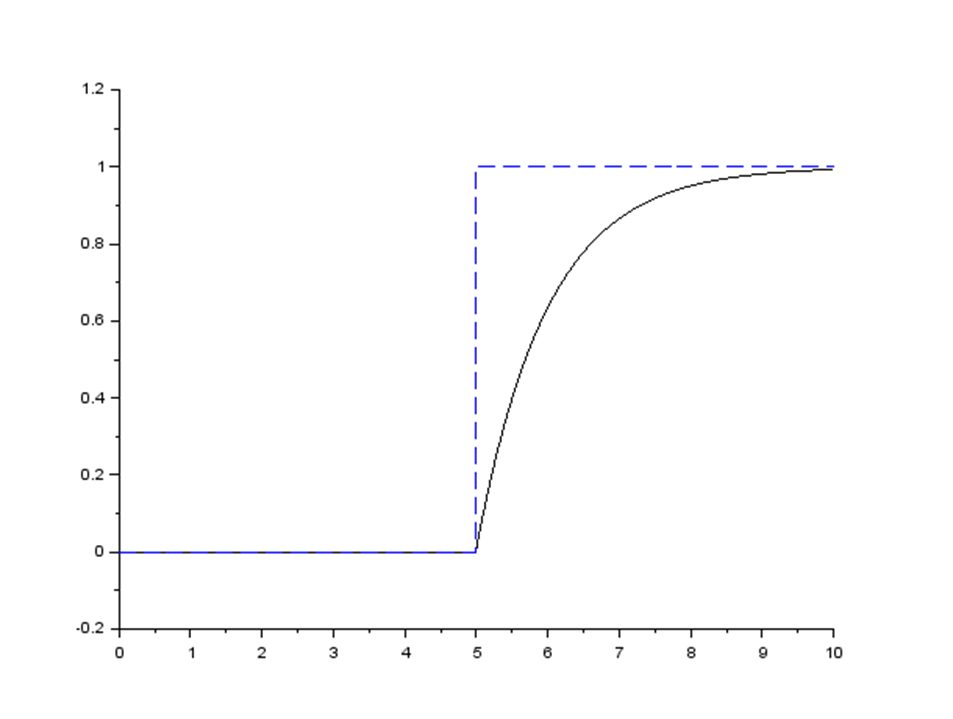

入力が制御で、
出力がその結果ってイメージ?

そのイメージであってるよ。
今回で仕様で言うと、
- アクセル開度が入力
- 車速が出力
と考えるとイメージしやすい

なるほど。
アクセスを一気に踏み込んでも、
すぐに車速には反映されないもんね。
それと同じ特性ってことだね。

そして、これを伝達関数で表現すると以下になる。
$$G(s)=\frac{c}{as+b}$$

これは、
もしやラプラス変換ってやつでは?

うん。
ここでは、\(s\)は微分、\(\displaystyle\frac{1}{s}\)は積分を示していると思って良い。

んー。
だとすると、
一次遅れ系は積分なような積分じゃないような?

まぁ、
積分的な性質は持っているが、
このままだと離散化する際に手間がかかるので、
変形しておく。

\(P\):出力
\(A_p\):アクセル開度
\(a\):時定数ゲイン
\(b\):負帰還ゲイン
\(c\):定常ゲイン
$$\frac{P}{A_p}=\frac{c}{as+b}$$
$$P(as+b)=cA_p$$
$$Pas+Pb=cA_p$$
$$Pas=cA_p-Pb$$
$$P=(cA_p-Pb)\frac{1}{a}\frac{1}{s}$$
ブロック線図にするとこんな感じ。
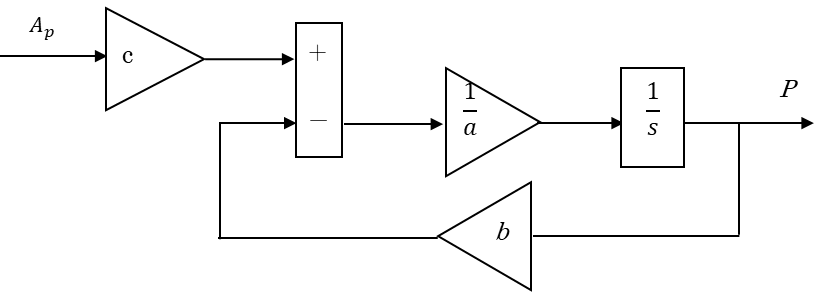

ん?
予想に反して結構シンプルだね。

まぁ
\(\displaystyle\frac{1}{s}\)の積分と\(b\)の負帰還ゲインが、
いろいろ吸収してしまっているのでシンプルに見えるかもね。

とりあえず、
これで車両の振る舞い相当になるってことで良いんだよね?

んー、
どうだろうか。
私のイメージだとアクセル開度と一次遅れ系の関係にあるのは車速ではなく、出力こと仕事率だと思うんだよね。

そーなの?
仮にそうだとして、
どうやって車速を表現したら良いの?

たぶん、仕事\(W[J]\)と仕事率\(P[W]\)の定義から算出できると思う。
仕事率から速度を求める

え!ちょっとやってみてよ!

こんな感じかな。
仕事\(W\)の定義より、
$$W=Fr$$
仕事率\(P\)の定義より、
$$P=W\frac{d}{dt}$$
これらより、
$$P=Fr\frac{d}{dt}$$
$$=mar\frac{d}{dt}$$
$$=mav$$
$$=ma^2t$$
$$a^2=\frac{P}{m}\frac{d}{dt}$$
$$a=\sqrt{\frac{P}{m}\frac{d}{dt}}$$
$$v=\int \sqrt{\frac{P}{m}\frac{d}{dt}} dt$$

算出できた!

ブロック線図で描くとこう。


この物理量の変換は以下のページを見ると分かるよ。

ということは先の一次遅れ系とつなげると・・・。

こんな感じで、
アクセル開度から車速が求められることになる。


すごい!
なんちゃって車両モデルの完成だ!

まぁ、
実際の車両の応答性から、
一次遅れ系の時定数ゲイン、負帰還ゲイン、定常ゲインを求めたり、
仕事率→車速変換のために質量(車体重量)を調べておく必要はあるけどね。

よし!あとはSimulinkにコピぺしt

ちょい待ち。

なに?

制御対象側も離散化してしてしまおう。

制御対象側も離散化しなきゃダメなの?

Simulinkでシミュレーションするだけだったら不要だろう。
ただ、今回はこれを簡易HILSにするんだろう?
だったら、ソフトウェア仕様として定義できるよう離散化は必要だろう。

なるほど。
そういえばそれがあったね。

というわけで、
次回は制御対象側の離散化をする。

オッケー
まとめ

まとめだよ。
- 制御対象はおおよそ一次遅れ系で表現できることが多い。
- アクセル開度と一次遅れ系の関係性を持っているのは出力。
- 出力(仕事率)から車速が算出できる。
バックナンバーはこちら




コメント