G検定記事はこちら。
https://www.simulationroom999.com/blog/jdla-deep-learning-for-general-2020-1/
はじめに
前回のボードゲームの続きに位置付けられる話。
ボードゲームに勝利する際は探索木とそのルート上の点数が重要になってくるが、この点数付けは人間が実施している。
よって、点数を付けた人次第で結果が左右される状態とも言える。
それを解消するためにモンテカルロ法という手法を用い始めた。
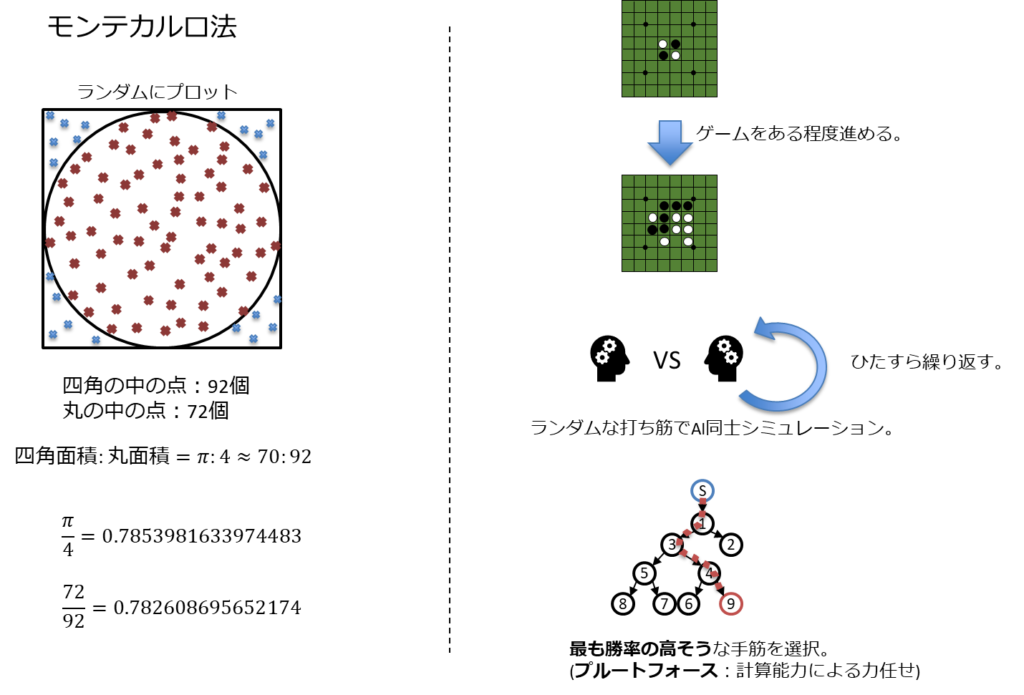
モンテカルロ法
端的に言うと、「乱数を使用してシミュレーションを繰り返し、確率論的に推定値を算出する手法」
つまり、答えはわからないが、ランダムにいろいろやって事象が収束すれば、それが答えである可能性が高いということを言っている。
円周率を確率論で算出するなどが割とおもしろい例として挙げられる。
円の面積は以下で表される。
$$S=πr^2$$
rを1とした場合、円の面積はπとなる。
該当円をぴったりと収める正方形の面積は以下となる。
$$(1×2)^2=4$$
よって、
$$円:正方形=π : 4$$
ここで、円が収まっている正方形内にランダムでプロットした結果は、以下になるはずである。
円の中のプロット:全プロット数
そして、これは
$$π:4$$
になるはず。
という感じ。
ボードゲームへの適用
モンテカルロ法をボードゲームに適用するには以下の方式になる。
- ゲームをある程度進める
- 途中でAI同時が仮想プレーヤーになって、ランダムな手を指すシミュレーションを実施して1回ゲーム終了とする
- プライアウトと呼ぶ
- プレイアウトを複数回実行して最も勝率が高いものを点数が高いものとする
これにより、人為的に点数付けを切り離し、確率論的な点数付けができるようになる。
計算能力を笠に着た力任せなやり方をブルートフォースと呼ぶ。
しかし、この手法も囲碁ではなかなか勝てない期間が存在している。
※最終的にはディープラーニングを使用したAlphaGoの登場待ちとなる。
まとめ
- 推論、探索の時代は、基本、「初期状態」「行動」「結果」が明確であることをベースにしている。
- 後期に入るとモンテカルロ法の方な確率論が導入され始める。
- 最終的には計算能力がモノを言う時代だったと言える。




コメント