MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第5章 その79【複素フーリエ係数④】
を書き直したもの。
複素フーリエ係数のシリーズ。
今回は、複素指数関数の直交性をプログラムで確認できるかの検討。
【再掲】複素フーリエ係数に至る道
まずは複素フーリエ係数に至る道を再掲。
- 複素指数関数の積
- 複素指数関数が直交していない状態
- 複素指数関数が直交している状態
- 複素指数関数の直交性の確認
- 複素フーリエ係数の導出
今回は、複素指数関数の直交性をプログラムで確認できるかの検討。
複素指数関数の直交性
前回までの式をまとめると以下になる。
\(
\displaystyle\int_{-\pi}^{\pi}e^{i(m-n)x}dx=
\begin{cases}
2\pi & (n =m) \\
0 & (n \neq m)
\end{cases}
\)
nとmが等しい時は\(2\pi\)、異なる時は\(0\)、
よって、実数フーリエ係数の時と同じで、
狙った角周波数の抽出可能な状態は作れるってことになる。
複素指数関数の直交性をアニメーションで
実数フーリエ係数の時もやったと思うが、
直交性をアニメーションで見てみよう。
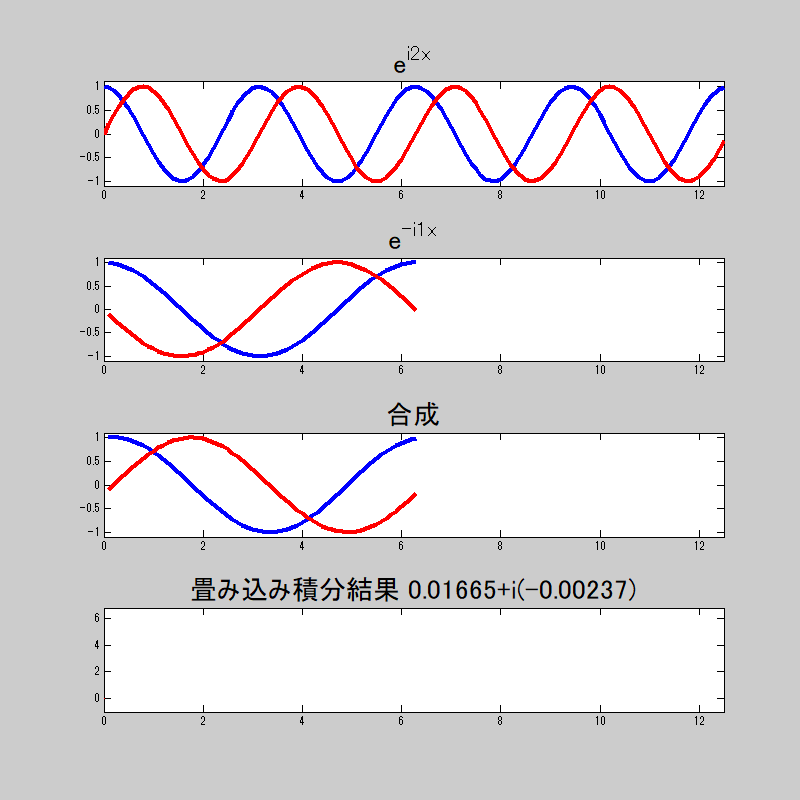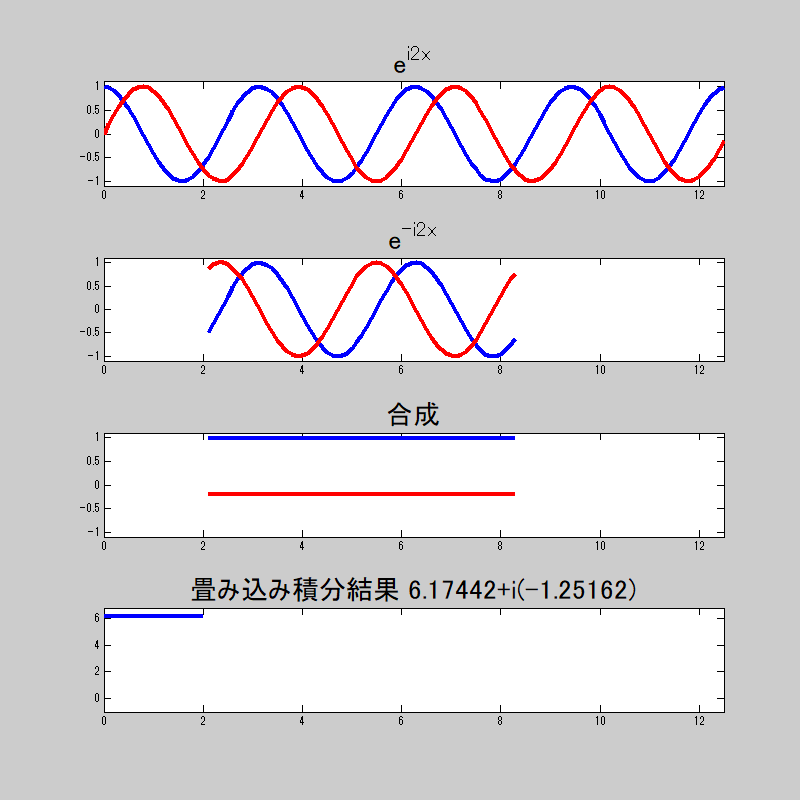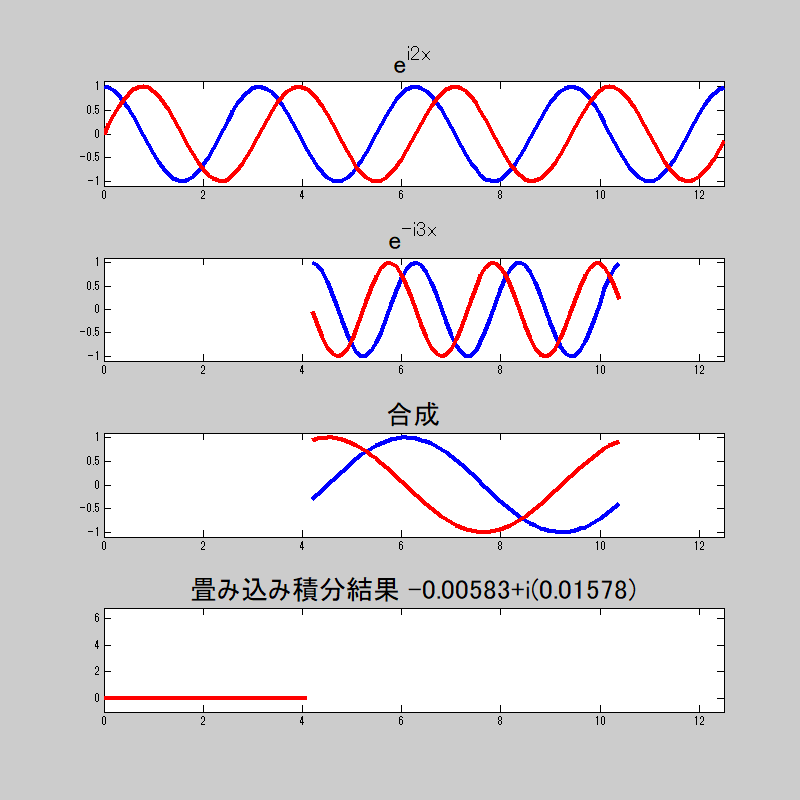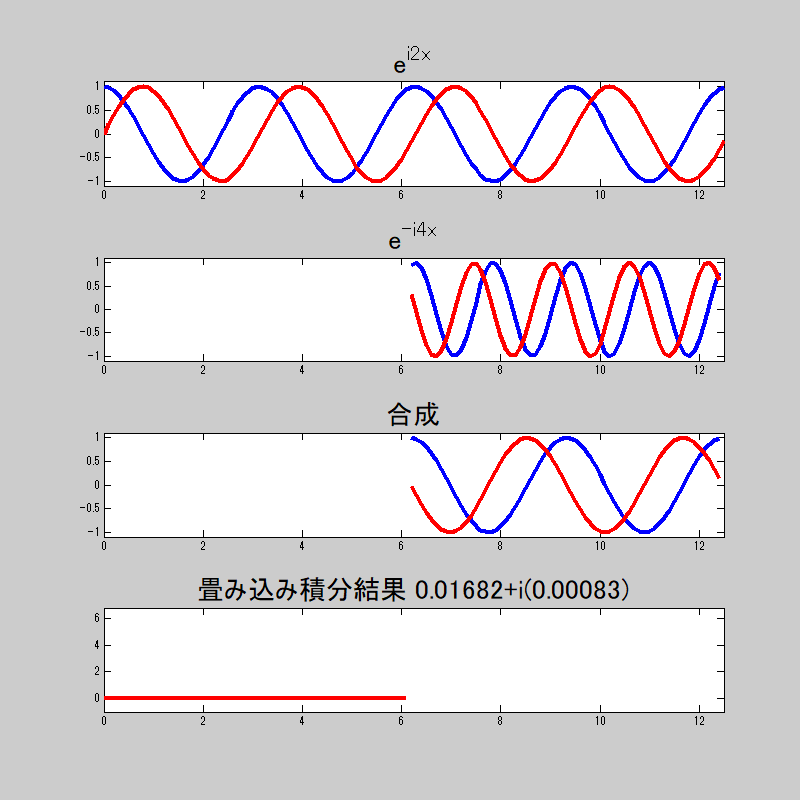
複素数だから、実数部と虚数部がある。
畳み込み積分をすると、等しい時は\(0\)、それ以外は\(2\pi\)になってるのがわかる。
若干誤差は出ているが、おおよそ狙った挙動はしていると思う。
プログラムで確認
複素指数関数の直交性をプログラムで確認してみよう。
実数フーリエ係数の時も似たようなことした。
ノリは全く一緒。
以下の式についてそれぞれ確認する。
\(
\begin{eqnarray}
e^{ix}\cdot e^{-ix}&=&6.28319\\
e^{ix}\cdot e^{-i2x}&=&0.00000\\
e^{i2x}\cdot e^{-i2x}&=&6.28319\\
e^{i3x}\cdot e^{-i2x}&=&0.00000
\end{eqnarray}
\)
等しい時と異なる時を確認ってことになる。
おそらく問題が出ることはないと思うが
各ツール、各言語で確認する。
まとめ
- 複素指数関数の直交性を評価できる式を確認。
- 直交性をアニメーションgifで見てみた。
- この直交性を各ツール、各言語で確認してみる。
MATLAB、Python、Scilab、Julia比較ページはこちら
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす





コメント