Sorry, you have Javascript Disabled! To see this page as it is meant to appear, please enable your Javascript!

MATLAB,Python,Scilab,Julia比較第5章その79【複素フーリエ係数④】

数値計算

MATLAB,Python,Scilab,Julia比較第5章その79【複素フーリエ係数④】

2024.12.03

バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia5-backnumber/

目次

はじめに
登場人物
複素フーリエ係数
複素指数関数の直交性
複素指数関数の直交性をアニメーションで
プログラムで確認
まとめ

はじめに

複素フーリエ係数のシリーズ。
今回は、複素指数関数の直交性をプログラムで確認できるかの検討。

登場人物

博識フクロウのフクさん

指差しフクロウ

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1

エンジニア歴8年の太郎くん

技術者太郎

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1

複素フーリエ係数

太郎くん

太郎くん

まずは複素フーリエ係数に至る道を再掲。

複素指数関数の積
複素指数関数が直交していない状態
複素指数関数が直交している状態
複素指数関数の直交性の確認
複素フーリエ係数の導出

フクさん

フクさん

今回は、複素指数関数の直交性をプログラムで確認できるかの検討。

複素指数関数の直交性

フクさん

フクさん

前回までの式をまとめると以下になる。

$\int_{- π}^{π} e^{i (m - n) x} d x = {\begin{cases} 2 π & (n = m) \\ 0 & (n \neq m) \end{cases}$

太郎くん

太郎くん

nとmが等しい時は $2 π$ 、異なる時は $0$ だから、
実数フーリエ係数の時と同じで、
狙った角周波数の抽出可能な状態は作れるってことか。

フクさん

フクさん

そうそう。

複素指数関数の直交性をアニメーションで

フクさん

フクさん

実数フーリエ係数の時もやったと思うが、
直交性をアニメーションで見てみよう。

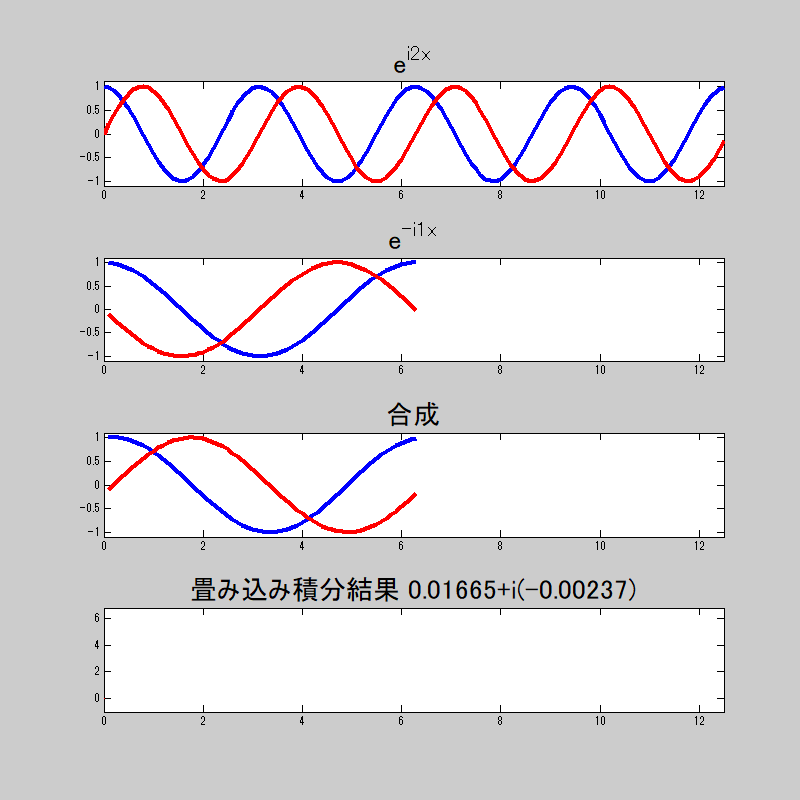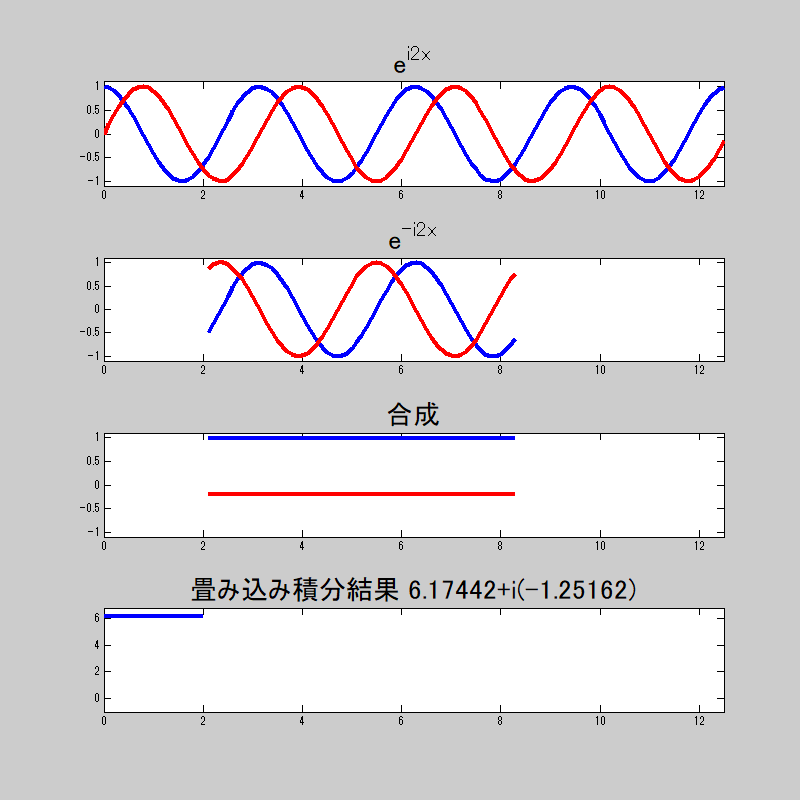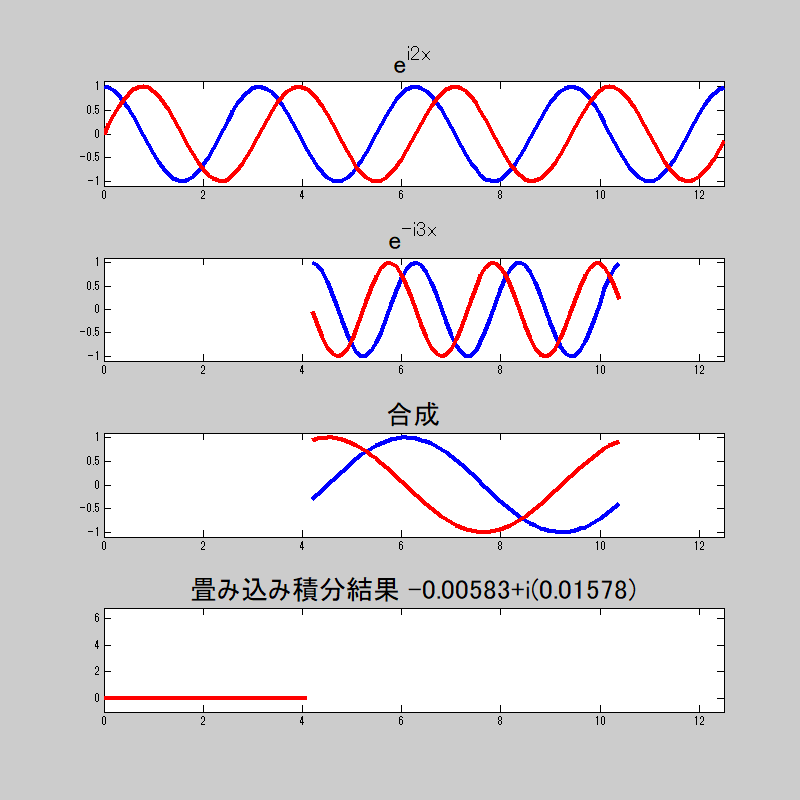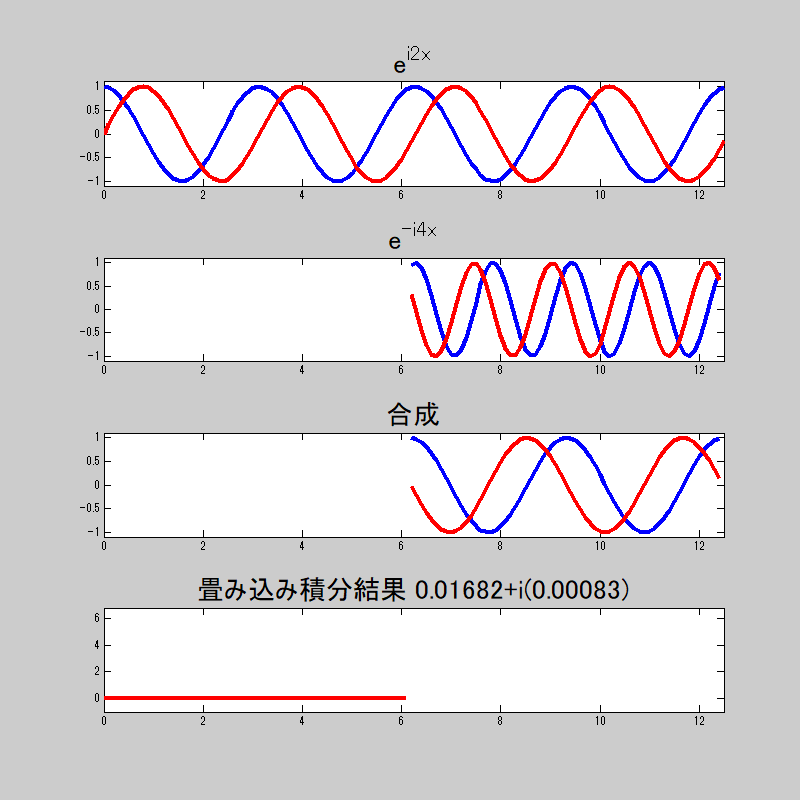
複素指数関数の直交性アニメーション

太郎くん

太郎くん

そうか。
複素数だから、実数部と虚数部があるのか。
畳み込み積分をすると、等しい時は $0$ 、それ以外は $2 π$ になってるのがわかるってことか。

フクさん

フクさん

若干誤差は出ているが、まぁおおよそ狙った挙動はしているな。

プログラムで確認

フクさん

フクさん

複素指数関数の直交性をプログラムで確認してみよう。

太郎くん

太郎くん

実数フーリエ係数の時も似たようなことしたね。

フクさん

フクさん

ノリは全く一緒だな。
以下の式についてそれぞれ確認する。

$\begin{array}{rcl} e^{i x} \cdot e^{- i x} & = & 6.28319 \\ e^{i x} \cdot e^{- i 2 x} & = & 0.00000 \\ e^{i 2 x} \cdot e^{- i 2 x} & = & 6.28319 \\ e^{i 3 x} \cdot e^{- i 2 x} & = & 0.00000 \end{array}$

太郎くん

太郎くん

等しい時と異なる時を確認って感じだね。

フクさん

フクさん

まぁ、問題が出ることはないと思うが
各ツール、各言語で確認だ。

まとめ

フクさん

フクさん

まとめだよ。

複素指数関数の直交性を評価できる式を確認。
直交性をアニメーションgifで見てみた。
この直交性を各ツール、各言語で確認してみる。

バックナンバーはこちら。

マンガでわかるフーリエ解析

手を動かしてまなぶフーリエ解析・ラプラス変換

手を動かしてまなぶフーリエ解析・ラプラス変換 | 山根英司 | 数学 | Kindleストア | Amazon

Amazonで山根英司の手を動かしてまなぶフーリエ解析・ラプラス変換。アマゾンならポイント還元本が多数。一度購入いただいた電子書籍は、KindleおよびFire端末、スマートフォンやタブレットなど、様々な端末でもお楽しみいただけます。

物理数学　量子力学のためのフーリエ解析・特殊関数

単位が取れるフーリエ解析ノート

今日から使えるフーリエ変換　普及版　式の意味を理解し、使いこなす

コメント

タイトルとURLをコピーしました