バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia5-backnumber/
はじめに
前回から複素フーリエ係数のシリーズに突入。
今回は「複素指数関数が直交していない状態」を確認。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
複素フーリエ係数

まずは複素フーリエ係数に至る道を再掲。
- 複素指数関数の積
- 複素指数関数が直交していない状態
- 複素指数関数が直交している状態
- 複素指数関数の直交性の確認
- 複素フーリエ係数の導出

今回は「複素指数関数が直交していない状態」を確認する。
複素指数関数同士の積の積分

まず、前回の指数関数の性質の式を再掲しておく。
\(
e^{imx}e^{-inx}=e^{m-n}x
\)

そして、以下の積分について考える。
\(
\displaystyle \int_{-\pi}^{\pi}e^{imx}e^{-inx}dx=\int_{-\pi}^{\pi}e^{i(m-n)x}dx
\)

指数関数の性質を考えると一つの指数関数にまとめられるのか。

まぁこれが複素フーリエ係数に繋がる式でもある。
複素指数関数が直交していない状態

そして、先ほどの式を評価することで直交評価ができる。

実数フーリエの時の三角関数同士の評価と同じと言えるのか。
確か、関数を無限次元ベクトルと解釈すると内積と同じになって、
0であれば直交、0でなければ直交していない。

まずはわかりやすい直交していない場合を考える。
答えとしては\(m=n\)の時は直交していないと言える。
代入した結果は以下になる。
\(
\begin{eqnarray}
\displaystyle \int_{-\pi}^{\pi}e^{i(m-m)x}dx&=&\int_{-\pi}^{\pi}e^0 dx\\
&=&\int_{-\pi}^{\pi}1\,\,dx\\
&=&2\pi
\end{eqnarray}
\)

指数部が0だと1になるのは分かるけど、
積分の結果が\(2\pi\)になる理由がわからん。

これは積分の範囲が\(-\pi\sim\pi\)の\(2\pi\)の範囲だからだね。
以下の図をイメージしてもらうと分かると思う。
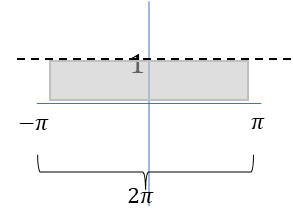

あ!そうか!
\(2\pi\times 1\)の長方形の面積になるから\(2\pi\)ってことなのか。

そうそう。

そして、内積の結果として0にならないことが証明された。

つまり、n=mの時は直交しない!
まとめ

まとめだよ。
- 複素指数関数同士の積の積分の式を提示。
- n=mの時の解を確認。
- 複素指数関数でn=mの時は直交しない。
バックナンバーはこちら。
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす




コメント