バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia5-backnumber/
はじめに
前回はマクローリン級数の説明。
今回は指数関数のマクローリン展開について。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】複素フーリエ級数に至る道

まずは複素フーリエ級数に至る道を再掲。
- テイラー級数
- マクローリン級数
- 指数関数のマクローリン展開
- cos(x)のマクローリン展開
- sin(x)のマクローリン展開
- オイラーの公式
- 複素フーリエ級数

今回は、指数関数のマクローリン展開。
マクローリン展開

マクローリン級数の話をしたが、
似たような言葉にマクローリン展開というものがある。

何か違うの?

ぶっちゃけ同じと思っても問題無いのだが、
厳密には異なる。
簡単に言うと、
マクローリン級数は形式的な級数展開であり、
マクローリン展開はその級数が実際に関数を表す場合を指すな。

(一体何が簡単だったのだろうか・・・。)

よくわからなければ、とりあえずは同じものと思ってもOKだ。
指数関数のマクローリン展開

試しに指数関数をマクローリン展開してみよう。
まずは\(e^x\)を微分しまくる
\(
\begin{eqnarray}
f(x)&=&e^x\\
f^{\prime}(x)&=&e^x\\
f^{\prime\prime}(x)&=&e^x\\
f^{\prime\prime\prime}(x)&=&e^x\\
\vdots
\end{eqnarray}
\)

という感じで変化しない。
つまり、以下と言える。
\(
f(0)=f^{\prime}(0)=f^{\prime\prime}(0)=f^{\prime\prime\prime}(0)=1
\)

指数部が0の時は必ず1になるからか。

よって、マクローリン展開で表現しなおすと以下になる。
\(
\begin{eqnarray}
\displaystyle f(x)&=&f(0)+\frac{f^\prime(0)}{1!}x+\frac{f^\prime\prime(0)}{2!}x^2+\dots\\
\displaystyle &=&f(0)+\sum_{n=1}^\infty\frac{f^n(0)}{n!}x^n\\
\displaystyle e^x&=&1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\dots\\
\displaystyle &=& \sum_{n=0}^\infty\frac{x^n}{n!}
\end{eqnarray}
\)

むちゃくちゃシンプルじゃん!
指数関数のマクローリン展開の式を元にプロット

ちなみに、nを徐々に増やしていくとこんな感じになる。
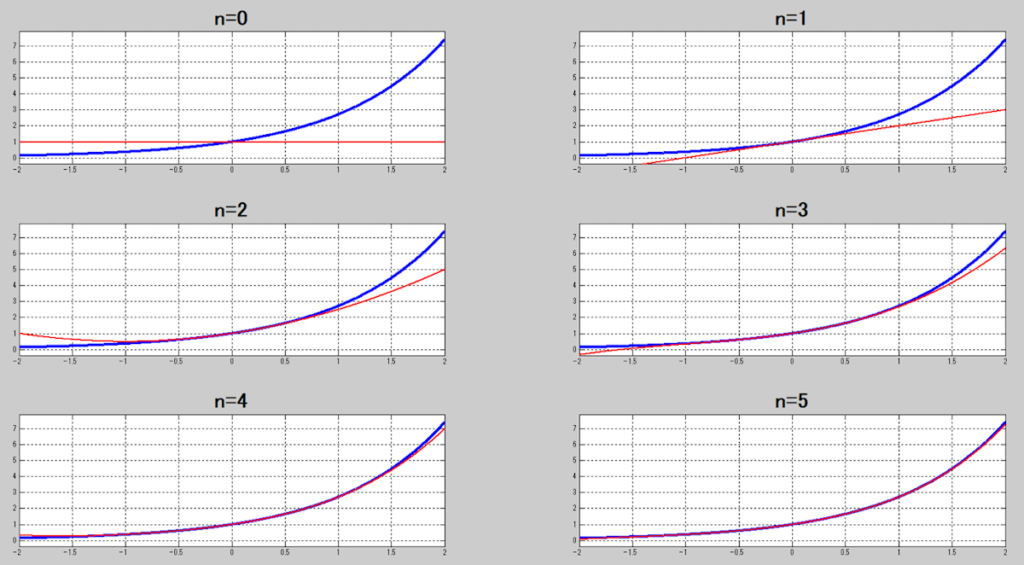

案の定ではあるけど、
nを増やしていけば近似度合いも上がっていくね。

こんな感じで、cos関数、sin関数もやっていく予定だ。
まとめ

まとめだよ。
- マクローリン展開について説明。
- 指数関数をマクローリン展開してみた。
- さらにマクローリン展開したものをグラフ化。
- nが増えれば近似度合いも上がる。
バックナンバーはこちら。
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす




コメント