MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第5章 その43【フーリエ係数⑦】
を書き直したもの。
フーリエ係数に至る道。
今回はフーリエ係数を求めるプログラムの話。
【再掲】フーリエ係数に至る道
まずは、フーリエ係数に至る道を再掲。
- 偶関数
- 奇関数
- 関数の内積
- 三角関数の加法定理
- 三角関数の積和公式
- 重要な極限値
- 三角関数の直交性
- フーリエ係数
今回はフーリエ係数の話の続きで
フーリエ係数を求めるプログラムの話。
フーリエ係数を求めるプログラム
とりあえず、フーリエ係数を求める式はわかったので、
いつもの流れで、プログラムを作成になる。
割とよくあるパターンとして、ノコギリ波とか矩形波のフーリエ係数を求めるのだが、
今回は、もう少し複雑な波形にしてみよう。
一見すると難易度が上げたように見えるが、
別に難易度は変わらない。
決まり切った波形ではなく、任意の波形を求められることを認識しようと思ったら、
少し複雑な方が認識しやすい。
少し複雑な波形
で、どんな波形に対して実施するかと言うと、
こんな波形。
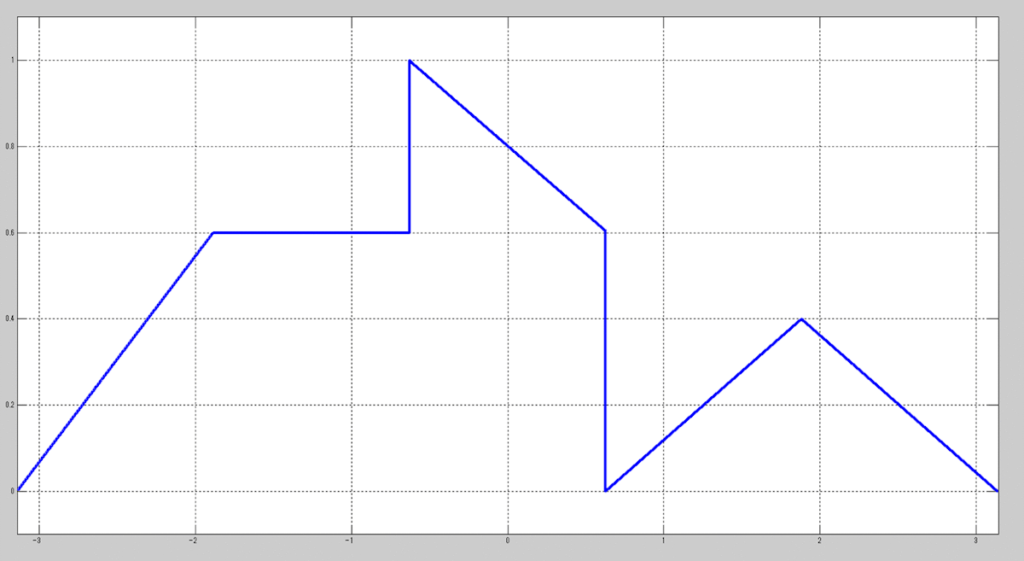
入力波形については、この波形に準じたcsvファイルを用意する。
そのcvsファイルを読み込んで、フーリエ係数を算出するって感じ。
一応、想定するプログラムのフローを記載しておこう。
- csvファイル読み込み
- 各種変数初期化
- フーリエ係数算出
- n=10,50,200のパターンでフーリエ級数で波形を合成
- グラフにプロット
ポイントn=10,50,200としてフーリエ級数で波形合成の部分。
n=が大きくなればなるほど、元の波形に近付くはず。
理想はn=∞だが、現実的にはそんなことはできない。
しかし、nを大きくしていくことで元の波形が再現できれば、
理屈としては通るってわけになる。
まとめ
- フーリエ係数を求めるプログラムを作成予定。
- フーリエ係数で係数を求め、その係数を利用してフーリエ級数で波形を再現する方式。
- nを大きくすることで、波形がどう変化するかがポイント。
MATLAB、Python、Scilab、Julia比較ページはこちら
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす





コメント