バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia5-backnumber/
はじめに
フーリエ係数に至る道。
今回はフーリエ係数の話の続き。
三角関数の直交性を利用した成分抽出の話になる。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】フーリエ係数に至る道

まずは、フーリエ係数に至る道を再掲。
- 偶関数
- 奇関数
- 関数の内積
- 三角関数の加法定理
- 三角関数の積和公式
- 重要な極限値
- 三角関数の直交性
- フーリエ係数

今回はフーリエ係数の話の続き。
三角関数の直交性を利用した三角関数成分の抽出

前回、ベクトルの成分の抽出の話をしたが、
それと、三角関数の直交性を組み合わせると、
三角関数成分の抽出が抽出可能となる。

何言ってるのかわからんのだけど・・・。

この話は正直文章では認識しずらい部分になる。
図示するのと数式で表現してみよう。
まず、以下の三角関数を持った関数があったとする。
\(
a\cdot\cos(x)+b\cdot\sin(x)
\)

この関数から、\(\cos,\sin)のそれぞれの成分を抽出したい。

抽出という言葉自体は、ベクトルの成分を抽出と似たようなこと言ってるけど、
うまく話が繋がらないな・・・。

ここで、横軸を\(\cos(x)\)、縦軸を\(\sin(x)\)とする平面を考え、
そこに先ほどの関数をベクトルとしておくと以下のように描ける。
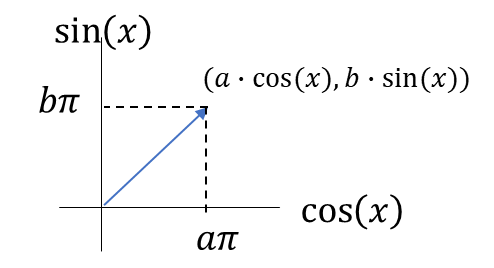

え゛。なにこの謎平面。

具体的にイメージしずらいとは思うが、
この平面は成立する。
少なくとも\(\cos(x)\)と\(\sin(x)\)は直交しているので、成立する。

確かに、直交性があるってことだから、成立すると言いきられるとそんか気もしてくるかな・・・。

これをベクトル演算を用いて、成分を抽出しようとすると以下の式になる。
\(
\begin{eqnarray}
\begin{bmatrix}
a\cdot\cos(x)&b\cdot\sin(x)
\end{bmatrix}
\begin{bmatrix}
1\cdot\cos(x)\\0
\end{bmatrix}&=&a\pi\\
\begin{bmatrix}
a\cdot\cos(x)&b\cdot\sin(x)
\end{bmatrix}
\begin{bmatrix}
0\\1\cdot\sin(x)
\end{bmatrix}&=&b\pi
\end{eqnarray}
\)

うーん、確かに、平面に記載して、
その基本ベクトルを元に抽出だから、
抽出できるという理屈もわからなくはないかな・・・。

\(\cos(x),\sin(x)\)を軸に取る部分がイメージしずらいと思うが、
重要なのは、同一の軸の基本ベクトルとの内積であれば、その成分が抽出できるという事実だ。
この点だけ覚えておけば良いだろう。
まとめ

まとめだよ。
- 三角関数の直交性を利用した三角関数成分の抽出について説明。
- イメージしずらい概念だが、関数の成分を抽出できるという事実に着目すると良い。
バックナンバーはこちら。
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす




コメント