バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia5-backnumber/
はじめに
フーリエ係数に至る道。
今回からフーリエ係数の話に突入。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】フーリエ係数に至る道

まずは、フーリエ係数に至る道を再掲。
- 偶関数
- 奇関数
- 関数の内積
- 三角関数の加法定理
- 三角関数の積和公式
- 重要な極限値
- 三角関数の直交性
- フーリエ係数

今回からフーリエ係数の話に突入する。
前回までに求めた三角関数の直交性を示す公式

フーリエ係数を求めるうえで重要なのが、
前回までに求めた三角関数の直交性を示す公式達になる。

確か、こんな式だよね。
\(
\begin{eqnarray}
&&\displaystyle\int_{-\pi}^{\pi}\sin(mx)\cos(nx)dx=0\\
&&\displaystyle\int_{-\pi}^{\pi}\sin(mx)\sin(nx)dx=
\cases{
\pi\dots \text{if } n=m\\
0\dots\text{if } n\neq m
}\\
&&\displaystyle\int_{-\pi}^{\pi}\cos(mx)\cos(nx)dx=
\cases{
\pi\dots \text{if } n=m\\
0\dots\text{if } n\neq m
}
\end{eqnarray}
\)

そうそう。
この公式により、\(\sin,\cos\)が直交していることの証明と
\(\sin\cdot\sin\)、\(\cos\cdot\cos\)、の解が\(0\)か\(\pi\)になることが証明された状態となる。
ベクトルの成分を抽出する理屈

フーリエ係数を求める上で、ベクトルからの成分抽出というのが重要な考え方となる。

成分抽出?

例えば、\((a,b)\)というベクトルがあり、
これの成分である\(a,b\)をそれぞれ抽出するにはどうすれば良いか。

いやー、見たまんまで\(a,b\)があるってことしか思いつかん・・・。

それを演算として求めるにはどうするかってことなんだが・・・。

まぁ、答えとしては、基本ベクトルとの内積を求めればOKという話となる。

基本ベクトル?

\((1,0)\)、\((0,1)\)みたいなものだな。
試しに図も交えながら、\(a,b\)が抽出されるイメージをとらえてみよう。
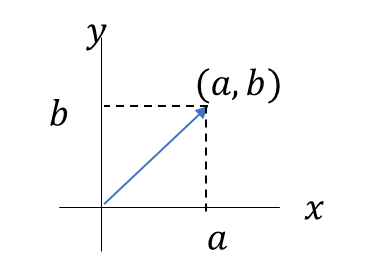
\(
\begin{eqnarray}
\begin{bmatrix}
a&b
\end{bmatrix}
\begin{bmatrix}
1\\0
\end{bmatrix}=a\\
\begin{bmatrix}
a&b
\end{bmatrix}
\begin{bmatrix}
0\\1
\end{bmatrix}=b
\end{eqnarray}
\)

あ、なるほど。
確かに\(a,b\)が抽出できる。

この感覚を別の軸且つ多変量な空間に対して行うのがフーリエ係数を求めるためのベクトルの内積となる。

(何言ってるのか全く分からねぇ・・・。)
まとめ

まとめだよ。
- 前回までに求めた三角関数の直交性を示す公式を再確認。
- ベクトルの内積によるベクトル成分抽出のイメージを説明。
バックナンバーはこちら。
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす




コメント