バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia5-backnumber/
はじめに
フーリエ係数に至る道。
今回は三角関数の直交性について説明。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】フーリエ係数に至る道

まずは、フーリエ係数に至る道を再掲。
- 偶関数
- 奇関数
- 関数の内積
- 三角関数の加法定理
- 三角関数の積和公式
- 重要な極限値
- 三角関数の直交性
- フーリエ係数

今回は三角関数の直交性について説明する。
直交性とは?

今回から三角関数の直交性の話になるが、
割とボリュームがある。

そもそも直交性って何?

まずはWikipediaから引用してみよう。
初等幾何学における直交(ちょっこう、英: orthogonal)は、「垂直に交わる」こと、すなわちユークリッド空間内の交わる二つの直線や平面のなす角が直角であることを意味する。
Wikipedia(https://ja.wikipedia.org/wiki/%E7%9B%B4%E4%BA%A4)

わかるような、わからんような・・・。

まぁ、名前の通りだな。
2つのベクトルが垂直に交わってる状態だ。

で、その直交性ってのが何に役立つの?

内積との兼ね合いで重要になる。
内積と直交性

2つのベクトルが直交している場合、それらのベクトルの内積は必ず0になる。

え?なんで?

内積をなす角で求める式を見てみよう。
\(
|a||b|\cos(\theta)
\)

ポイントはcos関数だな。
\(\cos(90^\circ)=0\)
つまり、内積の結果は必ず0になる。

なるほど。
cos関数の影響だったのか。

あとは、成分表記ベクトルで考えると
最もシンプルな直交したベクトルは\((0, 1)\)と\((1, 0)\)になる。
絵で示すと一目瞭然だろう。
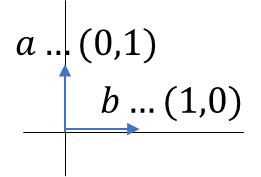

確かに垂直で交わってるね。

成分表記の内積を計算してみよう。
\(
\begin{bmatrix}
0&1
\end{bmatrix}
\begin{bmatrix}
1\\0
\end{bmatrix}=0
\)

当然な気がするけど、結果は0になるね。

これ以外にも直交するベクトルはあるが、
まずは直交しているベクトルの内積は0になることを覚えておこう。
まとめ

まとめだよ。
- 直交性とは2つのベクトルが垂直に交わることを指す。
- 直交しているベクトルの内積は必ず0になる。
- cos関数の影響。
- 成分表記の内積でも0になることを確認。
バックナンバーはこちら。
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす




コメント