MATLAB,Python,Scilab,Julia比較 第5章 その25【重要な極限値③】

バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia5-backnumber/

はじめに
登場人物
【再掲】フーリエ係数に至る道
【再掲】不等式のはさみうちの原理の結果
はさみうちの原理
sinc関数
まとめ

はじめに

フーリエ係数に至る道。
今回は重要な極限値について説明の続き。

登場人物

博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1

エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1

【再掲】フーリエ係数に至る道

太郎くん

まずは、フーリエ係数に至る道を再掲。

偶関数
奇関数
関数の内積
三角関数の加法定理
三角関数の積和公式
重要な極限値
三角関数の直交性
フーリエ係数

フクさん

今回は重要な極限値の説明の続きになる。

【再掲】不等式のはさみうちの原理の結果

フクさん

前回求めたものはこれだ。

\(
\begin{eqnarray}
\displaystyle 1 > \frac{\sin(x)}{x} &>& \cos(x) \\
\displaystyle \lim_{x\to0}\cos(x)&=&1\\
\displaystyle \lim_{x\to0}\frac{\sin(x)}{x}&=&1\dots(不等式のはさみうち原理により)
\end{eqnarray}
\)

太郎くん

はさみうちの原理ってなんだ？

はさみうちの原理

フクさん

はさみうちの原理についてはWikipediaを引用しよう。

はさみうちの原理（はさみうちのげんり）は、極限に関する定理の一つ。おおまかには、同じ極限値を持つ2つの関数に挟まれた第3の関数も同じ極限値を持つという主張である。
Wikipediaより(https://ja.wikipedia.org/wiki/%E3%81%AF%E3%81%95%E3%81%BF%E3%81%86%E3%81%A1%E3%81%AE%E5%8E%9F%E7%90%86)

太郎くん

これ見てもよくわからん・・・。

フクさん

ポイントは、以下の式だな。

\(
\displaystyle 1 > \frac{\sin(x)}{x} > \cos(x)
\)

フクさん

ここで、\(\cos(0)\)は\(1\)になる。
よって、\(\frac{\sin(x)}{x}\)も\(1\)に収束しないと辻褄が合わない。
って理屈だな。

太郎くん

なるほど。
言われてみれば確かにそうだ。

sinc関数

フクさん

今回扱った、\(\displaystyle\frac{\sin}{x}\)は
通称sinc関数と呼ばれるものだ。

太郎くん

そういう名前が付いているってことは割と重要な関数ってことになるのかな？

フクさん

今回のフーリエ係数にとっても重要なのだが、
ディジタル信号処理に於いても重要な関数のようだな。
まぁ、今回はそこには触れないが、
どのような波形になるかは確認しておこう。

太郎くん

確かに数式だけだされてもよくわからんよね。

フクさん

MATLABコードで書くとこんな感じだな。

sinc = @(x) sin(x)./x
x=-50:0.01:50
plot(x,sinc(x))
grid

フクさん

そして処理結果

太郎くん

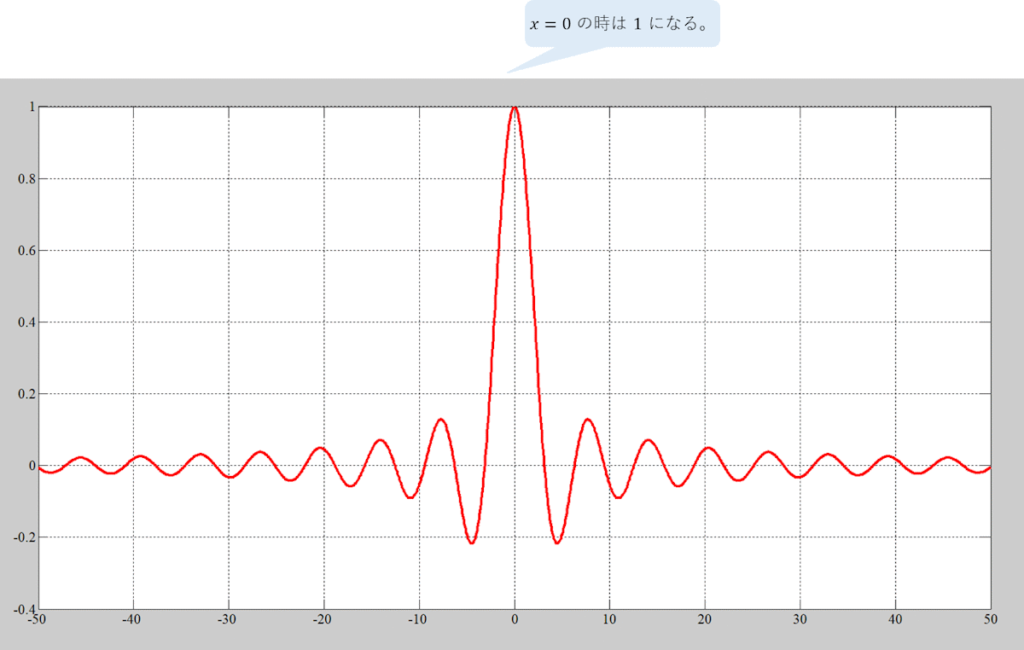
確かにxが0時は1になってるっぽいね。

フクさん

実際は、MATLABで演算した場合、sin(0)/0はNaNになるのだが、
0近辺が1に限りなく近いことはわかるだろう。
ちなみにPythonだと以下のコードだ。

import numpy as np
import matplotlib.pyplot as plt

def sinc(x):
    return np.sin(x)/x  

x = np.arange(-50, 50, 0.01)
plt.plot(x, sinc(x))
plt.grid(True)
plt.show()