MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第5章 その12【複雑な定積分②】
MATLAB,Python,Scilab,Julia比較 第5章 その13【複雑な定積分③】
を書き直したもの。
フーリエ係数に至る道。
今回は偶関数と奇関数を利用した数学パズルを割と真面目に解くバージョン。
【再掲】フーリエ係数に至る道
まずは、フーリエ係数に至る道を再掲。
- 偶関数
- 奇関数
- 関数の内積
- 三角関数の加法定理
- 三角関数の積和公式
- 重要な極限値
- 三角関数の直交性
- フーリエ係数
今回は偶関数と奇関数を利用した数学パズルを割と真面目に解くバージョン。
前回の数学パズルを真面目に解く?
前回は、なぞの定積分を偶関数と奇関数の特性を利用すると解けてしまうって話だった。
前回は、比較的大雑把に解いた感じ。
今回は、これを真面目に解いてみる。
数式を展開
まずは元の数式を展開する。
\(
\begin{eqnarray}
&&\displaystyle\int_{-2}^2\Big(x^3\cos(2x)+\frac{1}{2}\Big)\sqrt{4-x^2}dx\\
&=&\displaystyle\int_{-2}^2\Big(x^3\cos(2x)\sqrt{4-x^2}+\frac{1}{2}\sqrt{4-x^2}\Big)dx
\end{eqnarray}
\)
ここは普通にわかるだろう。
平方根の関数の正体を探る
ここで問題になるのか、
\(\sqrt{4-x^2}\)が何者かという点。
前回の話では、半円の方程式と説明した。
三平方の定理から求められるのだが、
少し図を交えて説明する必要がある。
まず三平方の定理を確認しよう。
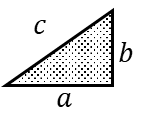
これを三平方の定理で表現すると以下になる。
\(
c^2=a^2+b^2
\)
ここも特に疑問は出ないだろう。
これを原点と円周の任意の点と、その点から垂直方向に落とした点を\(x\)で構成された三角形として考える。
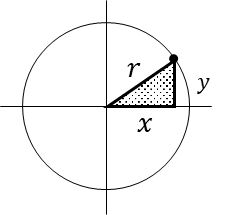
三平方の定理を使うと以下が成立する。
\(
r^2=x^2+y^2
\)
yとして解くと、
\(
y=\sqrt{r^2-x^2}
\)
つまり、\(\sqrt{4-x^2}\)は\(r=2\)の半円の方程式ということになる。
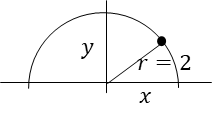
このような理屈で半円の方程式と特定できる。
半円なので、偶関数と言うことになる。
これでそれぞれの関数が偶関数、奇関数と判明したことになる。
あとは、偶関数、奇関数の特性を利用して解けば良い。
次のページへ
次のページで偶関数、奇関数の特性を利用して解く話。





コメント