バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia5-backnumber/
はじめに
フーリエ係数に至る道。
今回は奇関数の説明。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】フーリエ係数に至る道

まずは、フーリエ係数に至る道を再掲。
- 偶関数
- 奇関数
- 関数の内積
- 三角関数の加法定理
- 三角関数の積和公式
- 重要な極限値
- 三角関数の直交性
- フーリエ係数

今回は奇関数の説明について。
奇関数の定義

前回が偶関数だったから、それに似たような話だとは思うが、
名前からは予測がつかんな・・・。

これもWikipediaから引用しよう。
関数\(f(x)\)が奇関数であるとは、
Wikipediaより(https://ja.wikipedia.org/wiki/%E5%81%B6%E9%96%A2%E6%95%B0%E3%81%A8%E5%A5%87%E9%96%A2%E6%95%B0)
\(f(-x)=-f(x)\)
が任意の\(x\)について成立することである

案の定、定義を見てもわからんな・・・。

要は、
原点(\(x,y\)共に\(0\))に対して点対称になるのが奇関数。

偶関数の時と似たような説明だが、
偶関数が線対称に対して、奇関数は点対称??
やっぱりイメージがわかん。
奇関数の例

ならば、偶関数の時のように例を示そう。
代表的なものは以下2つ。
\(y=x^n\dots(ただしnは奇数であること)\)
\(y=\sin(x)\)

実際のグラフはこれになる。
\(y=x^5\)
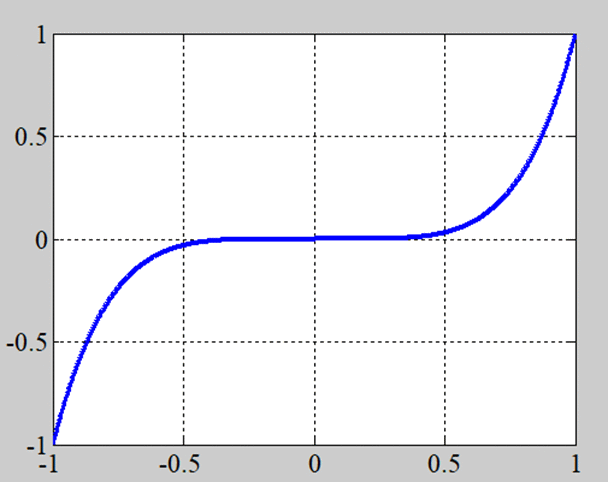
\(y=\sin(x)\)
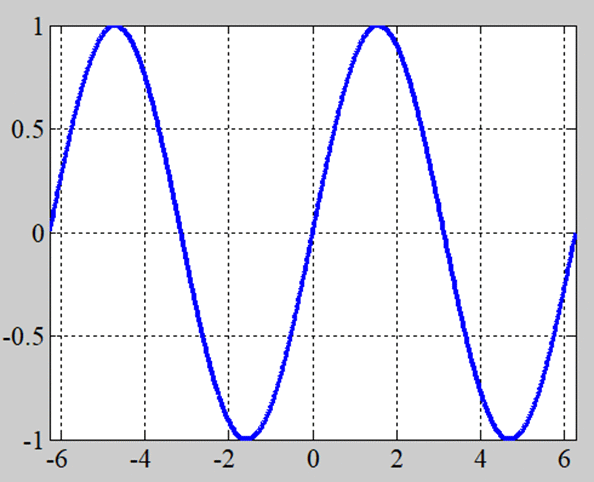

あー、なるほど。確かに点対称だ。

それに、べき乗関数の\(n\)が
偶関数の時は偶数。
奇関数の時は奇数。
になるのか。

そうそう。
そこが、偶関数、奇関数という名前がついた由来だろう。
奇関数の特性

そして、偶関数の時のように奇関数にも重要な特性がある。

偶関数の時みたいに定積分した場合の話?

そうそう。
\(x=0\)を中心として、\(-L\sim L\)の範囲で定積分をすると必ず0になる。

そうか。
さっきのグラフを見ると、点対称だから、プラス側の領域とマイナス側の領域が同じ面積になるのか。
だから、原点から同じ幅で見た場合の定積分は相殺されて0になる。
言われてみると当たり前な話だね。

その当たり前な話がいろいろ重要になってくるってことだな。
まとめ

まとめだよ。
- 奇関数について説明。
- 単純に原点に対して展対称な関数。
- この特性から-L~Lの範囲の定積分は、必ず0になる。
バックナンバーはこちら。
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす




コメント