バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia5-backnumber/
はじめに
フーリエ級数に至る道。
今回は波の合成について。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】フーリエ級数へ至る道

まずは、フーリエ級数へ至る道を再掲
- 無限級数
- 波の合成
- フーリエ級数

今回は、波の合成の説明になる。
波の合成

波の合成って名前からはイメージ沸かないな・・・。
勝手なイメージとしては積分使いまくりとかはあるけど・・・。

積分は使わないな。

何を使うの?

足し算。

え?それだけ?

もうちょっというと、三角関数の足し算だな。
まぁ、波が必ず三角関数というわけではないが、
周期性を持つ代表的な関数が三角関数であることと、
フーリエ級数に繋げる場合は、三角関数の合成の方が話としては近い。
というわけで、
波の合成≒三角関数の足し算
と思って良いかもね。

三角関数の足し算と言うと、
こんな感じ?
\(
sin(x)+sin(2x)+sin(3x)
\)

そうそう。
そのイメージだ。
波の合成結果

まぁ、三角関数を足すだけとはいわれたけど、
具体的にどうなるかはわからんな・・・。

実際に波形にするとこんな感じだな。
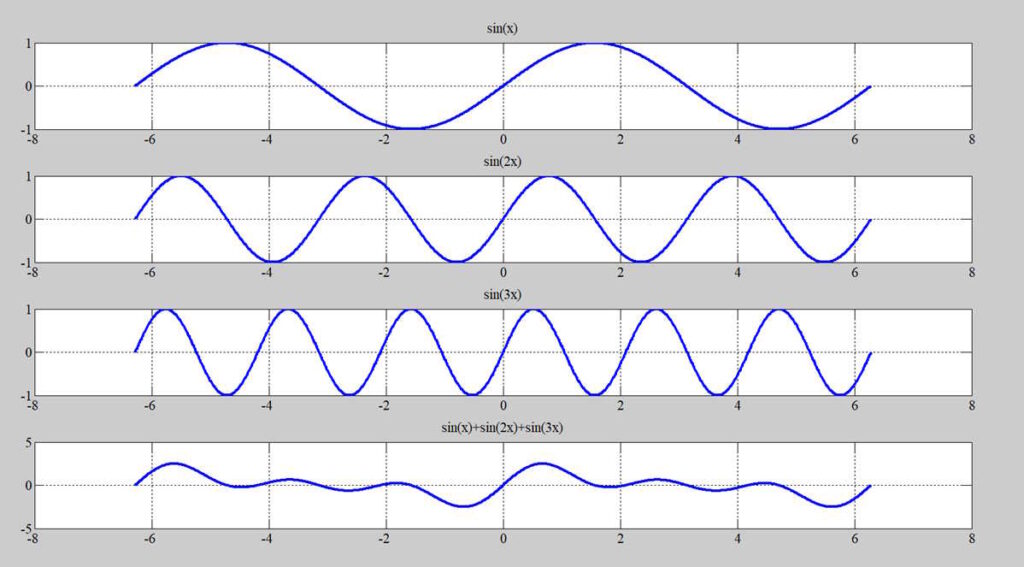

上から、sin(x)、sin(2x)、sin(3x)。
一番下がそれらを合成したものだな。

それぞれの単体の波形は当然のことながらシンプルだけど、
合成すると複雑になっていくのか。

そうそう。
これがフーリエ級数にとって重要な事象となる。
まとめ

まとめだよ。
- 波の合成について説明。
- 単なる関数の足し算になる。
- フーリエ級数に話を繋げるならば、三角関数の足し算と思えばOK。
バックナンバーはこちら。
マンガでわかるフーリエ解析
手を動かしてまなぶ フーリエ解析・ラプラス変換
物理数学 量子力学のためのフーリエ解析・特殊関数
単位が取れるフーリエ解析ノート
今日から使えるフーリエ変換 普及版 式の意味を理解し、使いこなす




コメント