バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
多層パーセプトロンの非線形分類時に局所最適解にハマってる現象が見られた。
対策としては、隠れ層のユニット数を増やすのが有効。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
隠れ層のユニット数を増やすと?

以前、実験した多層パーセプトロンは隠れ層のユニット数が2つだったんだよね。

そうそう。
これを増やせば、分類の表現力が上がって、局所最適解にハマりにくくなる。
まぁ、ハマりにくくなるというより、大域最適解に近い局所最適解が増えると思った方が正しいのだけど。

なるほど。
局所最適解にハマるという意味では一緒なんだけど、
分類としては問題無い局所最適解が出てくるってことか。

だから、分類時の決定境界線も複数のパターンが出てくると思う。
実際のユニット数

で、具体的なユニット数はどうするの?

まぁ、元々が2つだったわけだから、
3つか4つだな。
ここでは4つくらいにしておこう。
構成を図示すると以下になる。
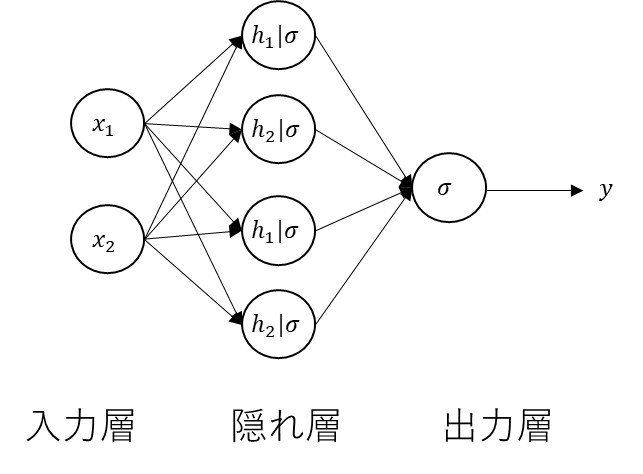

少し図が複雑になったので、バイアスや重みの表記は省略している。

理屈上は、これをもっと増やせるんだよな・・・。

入力層、出力層も増やせるから、とてつもなく複雑なこともできるはずってことだな。

そして、順伝播を無理やり行列演算的な表現にするとこんな感じになるな。
\(
y=
\sigma\Bigg(
\begin{bmatrix}
w_{211}&w_{212}&w_{213}&w_{214}&b_2
\end{bmatrix}
\begin{bmatrix}
\sigma\bigg(
\begin{bmatrix}
w_{111}&w_{112}&b_1\\
w_{121}&w_{122}&b_1\\
w_{131}&w_{132}&b_1\\
w_{141}&w_{142}&b_1\\
\end{bmatrix}
\begin{bmatrix}
x_1\\x_2\\1
\end{bmatrix}
\bigg)\\
1
\end{bmatrix}
\Bigg)
\)
プログラム的に調整するところ

で、プログラムとしてはどうなるの?
隠れ層を変えるわけだから、いろんなところが変わりそうな気がしてるんだけど?

MATLABコードでいうところの以下を変更すればOKなはずだ。
hidden_size = 2; % 隠れ層のユニット数↓
hidden_size = 4; % 隠れ層のユニット数
え?これだけ?

これだけ。

なんかこうもっと逆伝播の要素数を調整しないといけないとかいろいろありそうなもんだが・・・。

ベクトル、行列で演算が可能なツールや言語だと、そこらへんの辻褄合わせは楽なんだよね。
元々、要素数がいくつかは影響で無いように組むことが可能だ。

なるほど。
今回はその恩恵をバッチリ受けられるってことか。

あとは、プログラム上の変更ではないが、結果パターンが複数になることが想定されるので、
それらも確認する必要はあるな。

最初に言ってたやつだね。
どういうパターンが出てくるか知らんけど。
まとめ

まとめだよ。
- 多層パーセプトロンの隠れ層のユニット数を増やす。
- 表現力が上がるはず。
- 局所最適解にハマらないというより大域最適解に近い局所最適解が増えるというイメージ。
- プログラム上の修正点確認。
- ベクトル、行列演算ができるため修正範囲は極小。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント