バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
多層パーセプトロンの誤差逆伝播法を行い、非線形分類を行った。
しかし、実は問題点が・・・。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
非線形分類時の問題

多層パーセプトロンことニューラルネットワークでの非線形分類もバッチリな感じだね。

一見するとそうだな。

なんか含みがある言い方だな・・・。

実は現状の多層パーセプトロンだと一定の確率、およそ20%くらいで分類が失敗する。

え゛

ここは分類の成功パターンと失敗パターンを見てもらった方が早いな。
非線形分類の成功パターン

まずは成功パターン
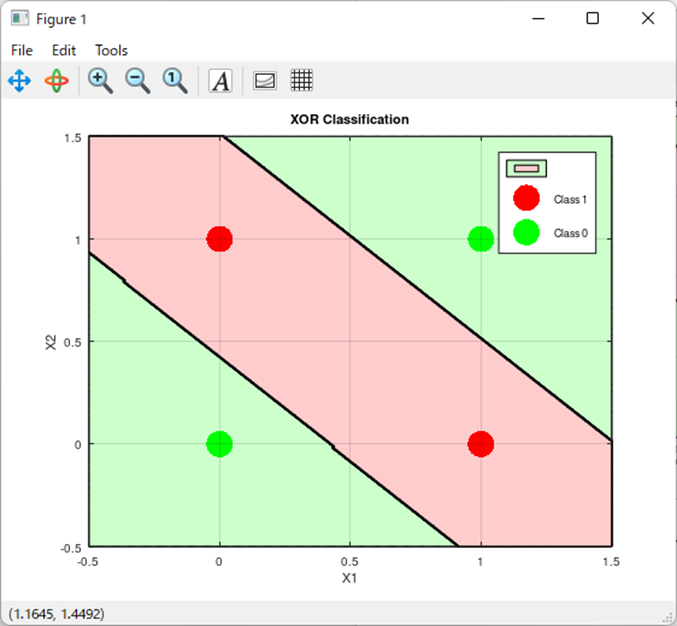

これは前回までで見てきたパターンだね。

かなり理想的に分類できていると言って良いだろう。
非線形分類の失敗パターン

そして、問題の失敗パターンはこれになる。
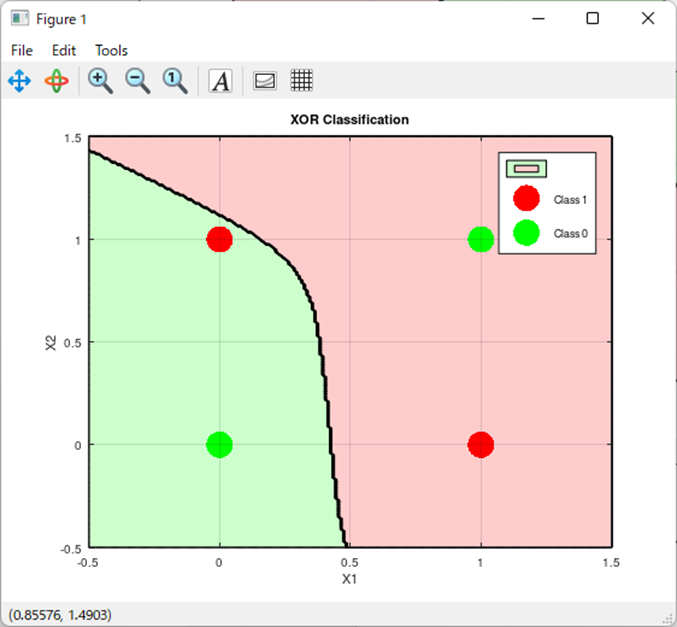

これは・・・。
分類できてない・・・。

これが一定の割合で発生するって感じだな。

発生すると言っても何が原因なのかもわからないから
対策の打ちようもないような・・・。

まぁ、ある程度推測はできるし、一般的な対策方法もあるから、
それを試してみるというのもありかな。

その一般的な対策をやってみるって感じ?

折角だから、その前にもう少し状況をモニタしたいところだな。
失敗パターンのモニタ方法

で、どうやってモニタするの?

シンプルなのは誤差関数の収束度合いの確認だな。
確認のポイントは以下だな。
- 最小値になっているか。
- 収束しているか、振動しているか。

最小値且つ収束になっていなければ、局所最適解にハマってるって感じかな。

そうだね。
振動しているようであれば、学習の回数であるエポック数が足りないとかになるな。
まぁ、今回の場合だと局所最適解にハマってるパターンだと思うけど。

これで状況の確認ができるってことか。

あとは、決定境界線の推移をアニメーションで見れるようしておくと分かり易いかもしれない。

分類に至るまでの過程が見えそうだね。

ここら辺を次回までに準備しておこう。
まとめ

まとめだよ。
- 非線形分類をしたが実は問題が発生している。
- 20%くらいの確率で分類ができない。
- 原因がわかるように誤差関数の推移や決定境界線の推移のアニメーションを見てみる予定。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント