バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
前回から、非線形分類の話に突入。
今回は、何を使って非線形分類を実現するかについて。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
非線形分類を実現

で、前回の疑問である、非線形分類を実現方法をどうするかってところかな。

多層パーセプトロンを使用する。

多層パーセプトロン?
名前的には単純パーセプトロンを複数にした感じ?

そうだね。
まぁ、「複数にする」という考え方には、並列にするか直列にするかという話があるけど。

で、どっちになるの?

両方だな。

(なんか一気に難易度が上がるような・・・。)
多層パーセプトロン

とりあえず、単純パーセプトロンと多層パーセプトロンの構造的な違いを確認しておこう。

まぁ、差分を知るのが一番手っ取り早そうだよね。

まずは単純パーセプトロン
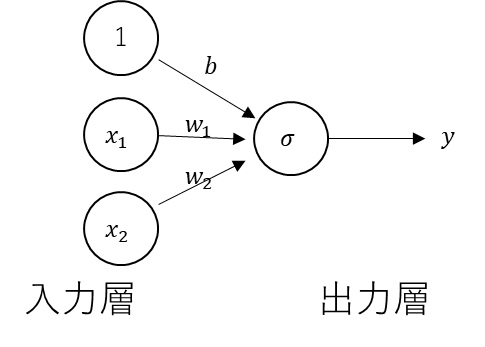

そして、これをベクトル演算で表現するとこんな感じ。
\(
y=\sigma\bigg(
\begin{bmatrix}
w_1&w_2&b
\end{bmatrix}
\begin{bmatrix}
x_1\\x_2\\1
\end{bmatrix}
\bigg)
\)

活性化関数の話はあるけど、基本的には単なる内積なんだよね。

そして、多層パーセプトロン
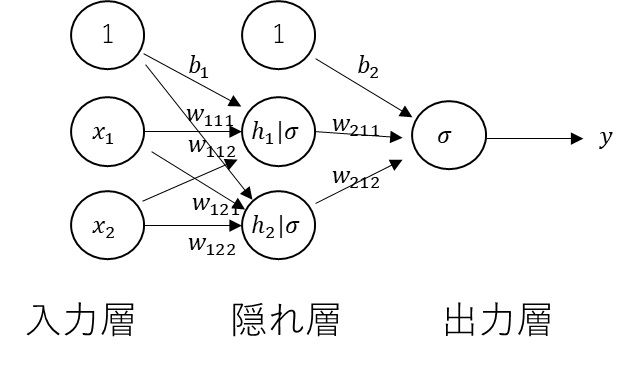

これも行列演算で表現してみよう。
\(
y=
\sigma\Bigg(
\begin{bmatrix}
w_{211}&w_{212}&b_2
\end{bmatrix}
\begin{bmatrix}
\sigma\bigg(
\begin{bmatrix}
w_{111}&w_{112}&b_1\\
w_{121}&w_{122}&b_1
\end{bmatrix}
\bigg)
\begin{bmatrix}
x_1\\
x_2\\
1
\end{bmatrix}\\
1
\end{bmatrix}
\Bigg)
\)

なんかやべぇことになってんな・・・。

まぁ、一般的にはこういう書き方はしないな。
無理やり書くとこんな感じって程度だ。

ちなみに多層パーセプトロンはニューラルネットワークとも言う。

あ、これがニューラルネットワークになるのか!
なんかテンションあがる!

最も原始的なニューラルネットワークだけどね。
まとめ

まとめだよ。
- 非線形分類するにはパーセプトロンを複数使う。
- つまり多層パーセプトロンにする。
- 単純パーセプトロン、多層パーセプトロンの構造と数式を説明。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント