バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
単純パーセプトロンで分類を行う。
今回はScilabで実現。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
単純パーセプトロンで分類のプログラムのフロー【再掲】

単純パーセプトロンで分類するプログラムのフローを再掲。
- データセットの定義
- ハイパーパラメータの設定
- 学習率
- エポック数
- パラメータの初期値、
- シグモイド関数の導関数の定義
- 順伝播
- 誤差計測
- 逆伝播
- バイアスの逆伝播
- 重みの逆伝播
- パラメータの更新
- 重みの変化の経緯をplot
重みとバイアスへの連鎖律への共通式
\(
\begin{eqnarray}
\displaystyle dZ&=&\frac{\partial E}{\partial A}\frac{\partial A}{\partial Z}=(A-Y)\cdot\sigma(Z)\{1-\sigma(Z)\}\cdot X\\
&=&
\Bigg(
\begin{bmatrix}
a_1\\a_2\\a_3\\a_4
\end{bmatrix}-
\begin{bmatrix}
0\\0\\0\\1
\end{bmatrix}
\Bigg)\circ
\sigma\Bigg(
\begin{bmatrix}
z_1\\z_2\\z_3\\z_4
\end{bmatrix}
\Bigg\{
1-\sigma\Bigg(
\begin{bmatrix}
z_1\\z_2\\z_3\\z_4
\end{bmatrix}
\Bigg)
\Bigg\}
\end{eqnarray}
\)
重みへの連鎖律
\(
\displaystyle\frac{\partial E}{\partial W}=dZ^TX=
\begin{bmatrix}
dz_1\\dz_2\\dz_3\\dz_4
\end{bmatrix}^T
\begin{bmatrix}
0&0\\
0&1\\
1&0\\
1&1\\
\end{bmatrix}
\)
バイアスの連鎖律
\(
\displaystyle\frac{\partial E}{\partial b}=\sum dZ=
\begin{bmatrix}
dz_1\\dz_2\\dz_3\\dz_4
\end{bmatrix}^T
\begin{bmatrix}
1\\1\\1\\1
\end{bmatrix}
\)

これをScilabで実現する。
Scilabコード

Scilabコードは以下。
function y = sigmoid(x)
y = 1./(1 + exp(-x));
endfunction
function y = sigmoid_derivative(x)
y = sigmoid(x) .* (1 - sigmoid(x));
endfunction
// データセットの定義
X = [0 0; 0 1; 1 0; 1 1];
Y = [0; 0; 0; 1];
// ハイパーパラメータの設定
learning_rate = 0.5; // 学習率の調整
num_epochs = 200; // エポック数の調整
// パラメータの初期化
W = rand(1, size(X, 2));
b = rand();
for epoch = 1:num_epochs
// 順伝播
Z = X * W' + b;
A = sigmoid(Z);
// 誤差計算
loss = mean((A - Y).^2);
// 逆伝播
dZ = (A - Y) .* sigmoid_derivative(Z);
dW = dZ' * X;
db = sum(dZ);
// パラメータの更新
W = W - learning_rate * dW;
b = b - learning_rate * db;
end
printf('W=');disp(W);
printf('b=');disp(b);
scatter(X(Y==0, 1), X(Y==0, 2), 100, 'r', 'fill');
scatter(X(Y==1, 1), X(Y==1, 2), 100, 'b', 'fill');
x1 = [min(X(:, 1))-1 max(X(:, 1))+1];
x2 = -(W(1)*x1 + b) / W(2);
plot(x1, x2, 'k', 'LineWidth', 2);
p=gca();
p.data_bounds(:,1)=[-0.5;1.5];
p.data_bounds(:,2)=[-0.5;1.5];
title(sprintf('Epoch: %d, Loss: %.4f', epoch, loss));
legend('Class 0', 'Class 1', 'Decision Boundary');
xgrid
処理結果

処理結果は以下。
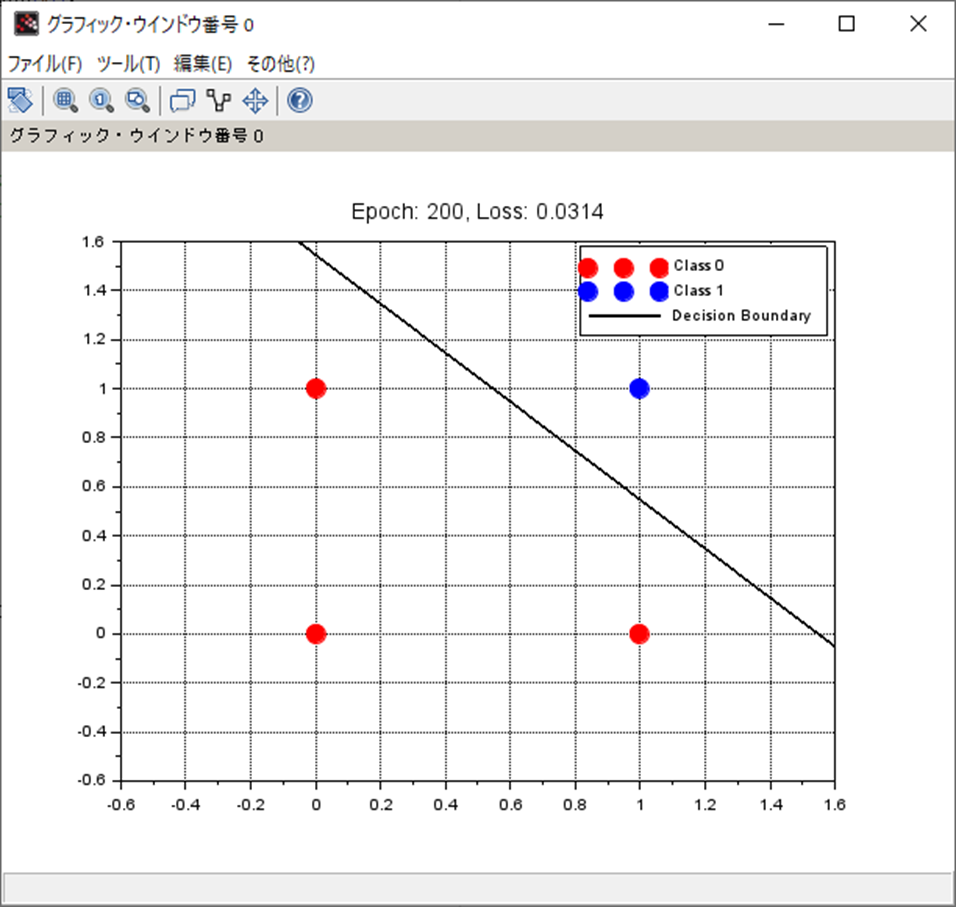
W=
2.6589781 2.6604184
b=
-4.1141813まとめ

まとめだよ。
- 単純パーセプトロンの分類をScilabで実施。
- 想定通り分類可能。
- おおよそ200エポックあれば分類可能。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント