MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第4章 その46【勾配降下法④】
を書き直したもの。
勾配降下法をプログラム的に確認する。
今回はMATLAB。
【再掲】勾配降下法の確認プログラムのフロー
とりあえず、勾配降下法の確認プログラムのフローを再掲
- 目的関数の定義
- 目的関数の導関数の定義
- 入力初期値設定
- ハイパーパラメータの設定
- 勾配降下法の実装
- 結果表示
- グラフへのプロット
これをMATLABで実施する。
MATLABコード
MATLABコードは以下。
% 目的関数の定義(例: f(x) = sin(5x) + 0.5x^2)
f = @(x) sin(5*x) + 0.5*x.^2;
% 目的関数の微分(例: df(x)/dx = 5cos(5x) + x)
df = @(x) 5*cos(5*x) + x;
% 初期値の設定
x = 2.9; % 初期値
% ハイパーパラメータの設定
learning_rate = 0.1; % 学習率
max_iterations = 100; % 最大イテレーション数
% 学習過程を保存するための変数
x_history = zeros(1, max_iterations);
f_history = zeros(1, max_iterations);
% 勾配降下法の実装
for i = 1:max_iterations
% 勾配の計算
gradient = df(x);
% パラメータの更新
x = x - learning_rate * gradient;
% 学習過程の保存
x_history(i) = x;
f_history(i) = f(x);
end
% 結果の表示
disp('optimal solution:');
disp(x);
disp('optimal value:');
disp(f(x));
% グラフのプロット
figure;
subplot(2, 1, 1);
x_vals = linspace(-3, 3, 100);
f_vals = f(x_vals);
plot(x_vals, f_vals);
hold on;
scatter(x_history, f_history, 'r');
xlabel('x');
ylabel('f(x)');
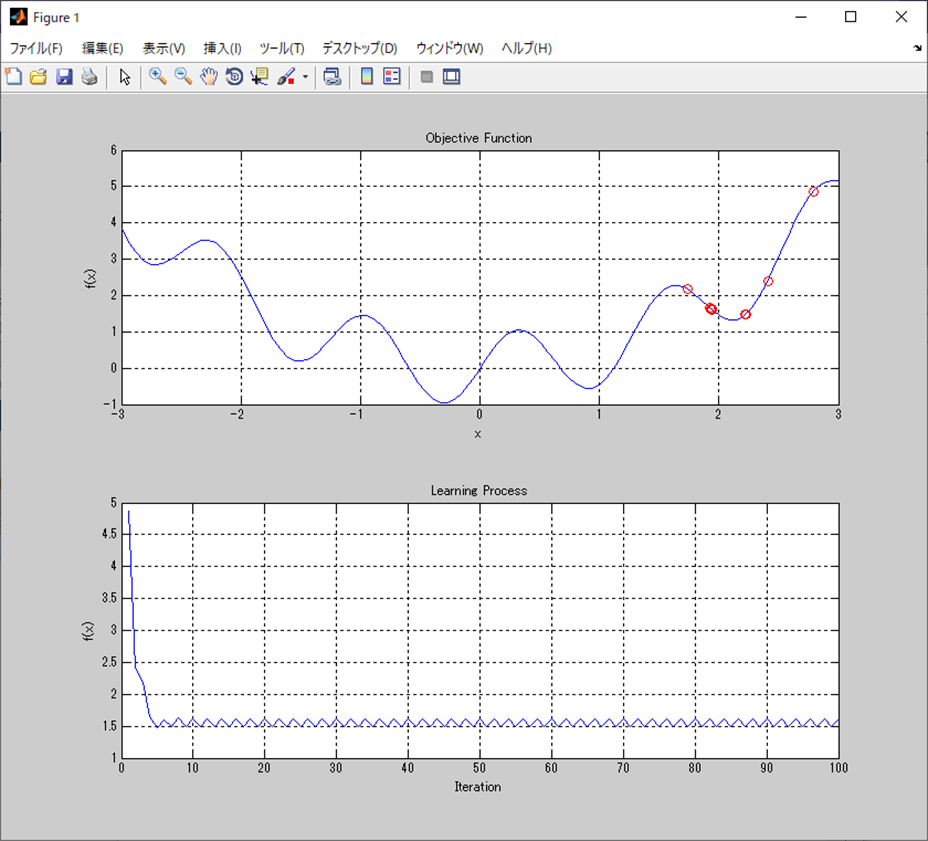
title('Objective Function');
grid;
subplot(2, 1, 2);
plot(1:max_iterations, f_history);
xlabel('Iteration');
ylabel('f(x)');
title('Learning Process');
grid;処理結果
処理結果は以下。
optimal solution:
1.9360
optimal value:
1.6214考察
案の上ではあるが、局所最適解に陥ってる状態。
最終的には入力が1.9360、その出力が1.6214。
これの解決したいところだが、
一般的には学習率を大きくすると、
山を越えて、次の谷を探しに行けるが、
問題は、この山を越えられる学習率に設定すると、
大域最適解の前後にある山も越えられてしまう。
というわけで、これだけでは全く解決しない。
これに関しては様々な最適化アルゴリズムが考案されている。
代表的なものは、以下。
- モーメンタム
- 過去の傾きに応じて学習率を補正して傾きが小さくなると学習率も小さくなる。
- AdaGrad
- 2次の勾配の累積の平方根を分母にし、学習率を調整
- Adam
- 1次の勾配と2次の勾配の指数平均移動をとり、2次の平方根を分母、1次を分子として学習率を調整
つまり、学習率を固定にしないで、勾配に応じて調整する。
基本的な考え方は、モーメンタムを見た方が良いだろう。
Adam以降の最適化アルゴリズムもあるが、Adamベースであることが多い。
まとめ
- 勾配降下法の実験をMATLABで実施。
- 予想通り局所最適解に陥った。
- 局所最適解の回避方法としては学習率を状況に応じて変更する様々は最適化アルゴリズムがある。
- モーメンタム、AdaGrad、Adamなどなど。
MATLAB、Python、Scilab、Julia比較ページはこちら
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析





コメント