はじめに
※ 本記事の以下を親記事とした子記事に位置付けられる。
https://www.simulationroom999.com/blog/physical-value-conversion/
前回、体積ベースの吸気流速\([L/sec]\)を質量ベースの吸気流速\([g/sec]\)に変換した。
今回はこの質量ベースの吸気流速\([g/sec]\)を実際の質量としての吸気流量\([g]\)に変換する。
流速流量変換
吸気流速\(M_{air} [g/sec]\) → 吸気流量\(G_{air} [g]\)を求める。
$$M_{air}[g/sec] →G_{air} [g]$$
\(M_{air}\)は\(G_{air}\)の変化量である。
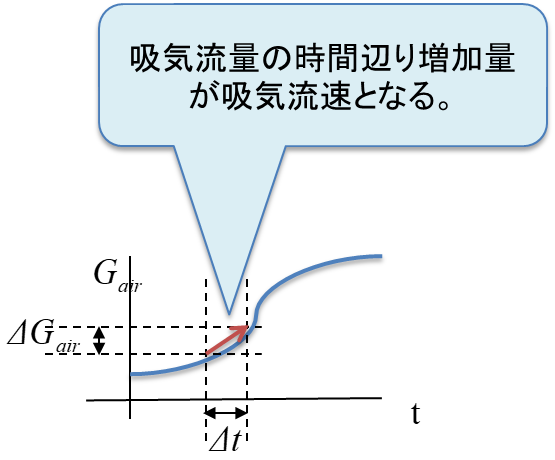
例えば、\(1[sec]\)の「\(G_{air}\)の変化量」\(ΔG_{air}\)は\(M_{air}\)そのものである。
$$M_{air}[g/sec]=\frac{ΔG_{air}[g]}{1[sec]}$$
つまり、時間次元合わせをすると以下が成立する
$$M_{air}[g/sec]=\frac{ΔG_{air}[g]}{Δt[sec]}$$
微小時間に於いても成立することは予測に固いため以下も成立する。
$$M_{air}[g/sec]=G_{air}[g]\frac{d}{dt[sec]}$$
よって、両辺を積分して以下。
※ 初期条件\(G_{air}(0)\)は\(0\)とし、積分定数も\(0\)ということにしておく。
$$\displaystyle \int M_{air}[g/sec]dt[sec]=G_{air}[g]$$
要は、\(M_{air}\)を積分すれば\(G_{air}\)が得られる。
吸気タイミング、取得タイミングを意識した流速流量変換
吸気周期は\(2[round]\)であり、\(24[msec]\)である。
エアフロメータ出力電圧取得タイミング クランク角 \(30°\)毎であることから、以下の式が成立する
$$\frac{360[deg/round]×2[round]}{30[deg]}=24$$
つまり、吸気周期\(24[msec]\)間にに\(24[回]\)のサンプリングが可能である。
よって、サンプリング周期は\(1[msec]\)となる。
数値積分(総和法)を適用し以下とする。
$$\displaystyle \int_{0[msec]}^{24[msec]}M_{air}[g/sec]dt[sec]≒\sum_{n=1}^{24}Mn_{air}[g/sec]Δt[sec]=\sum_{n=1}^{24}Mn_{air}[g/sec]×0.001[sec]$$
吸気流速\(M_{air}[g/sec]\) → 吸気流量\(G_{air}[g]\)変換:\(G(x)\)は以下となる。
$$G(x)=0.001[sec]×\displaystyle \sum_{n=1}^{24}x[g/sec]$$
まとめ
- 流速は流量の変化量である
- よって、流量を得るには流速を積分する必要がある
- しかし、エアフロメータからのセンサ値取得タイミングや実際の吸気工程のタイミングを意識した積分が必要。
おまけ(吸気工程周期が固定ではない場合。というかこっちが実用的な方)
今回は吸気工程周期を固定的に扱ったが、実際は固定ということは無い。
よって、現実的な式は以下になる。
クランク\(30°\)毎の平均時間:\(Δt\)
$$G(x,Δt)=Δt[sec]×\displaystyle \sum_{n=1}^{24}x[g/sec]$$




コメント