バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
連鎖律を把握するための解説。
多変量関数の連鎖律に突入
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】連鎖律を把握するための知識

まずは、連鎖律を把握するための知識を再掲
- 逆数の微分公式(済)
- 積の微分公式(済)
- 商の微分公式(済)
- シグモイド関数の導関数(済)
- 多変量関数の連鎖律
- 勾配降下法

今回は、多変量関数の連鎖律に突入・・・。
なのだが、これは割とボリュームがある。

マジかよ。

「多変量関数の連鎖律」に必要な知識を分解すると以下になる。
- 合成関数
- 合成関数の微分(連鎖律)
- 多変数関数の連鎖律
- 学習データの多入力による暗黙的関数追加

必要なものが増えやがった・・・。

まぁ、これも各個撃破だな。
合成関数

まずは合成関数。
これは名前の通り、合成した関数だ。

その「合成した関数」ってのが全く分からんのだけど・・・。

図示するとこれになる。
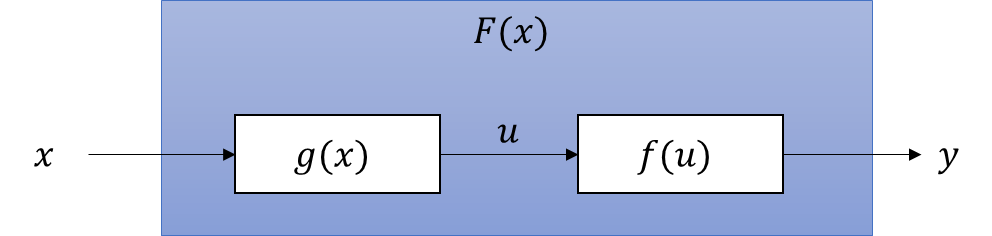

そして、これを数式で示したのがこれ。
\(
\begin{eqnarray}
y&=&f(x)\\
y&=&f(g(x))\\
F(x)&=&f(g(x))
\end{eqnarray}
\)

なんだ、関数の入力に関数を入れ込む感じか。

この例では2つの関数を合成しているが、
これが3つ、4つになってもOKだ。
そして、単純パーセプトロンは入力層の内積、活性化関数、誤差関数がそれぞれ関数と見なせる。

つまり、合成関数で表現可能ってこと?

そうそう。
まぁ、実際は多変量な入力を受け付けるので、これだけでは表現できないのだが、
ここで重要なのは関数がネストしていることと一緒という点を認識できればOKだ。

雰囲気だけはわかった。
まとめ

まとめだよ。
- 多変数関数の連鎖律に突入したが、これを理解するのに必要な知識があるため、それらを列挙。
- 合成関数について説明。
- 単純パーセプトロンも入力層の内積、活性化関数、誤差関数の組み合わせが合成関数と言える。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント