はじめに
※ 本記事の以下を親記事とした子記事に位置付けられる。
https://www.simulationroom999.com/blog/physical-value-conversion/
エアフロメータから吸気流量を求める際に必要な変換として体積質量変換がある。
これについて紐解いていく。
体積質量変換
吸気流速\(V_{air} [L/sec]\) と 吸気流速\(M_{air} [g/sec]\) の差異は、体積\(V[L]\)と質量\(m[g]\)である。
よって、体積から質量への変換ができれば良いと言える。
しかし、体積は温度、気圧の影響を受ける
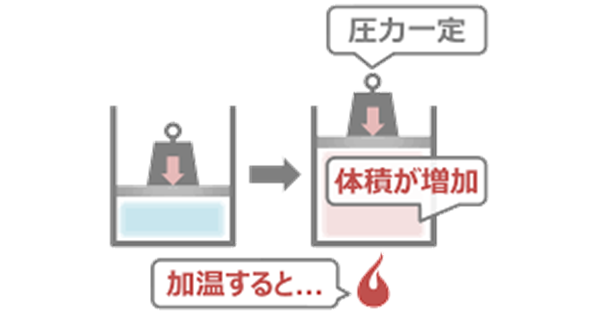
よって、変換式は以下が想定される。
体積質量変換式:\(f(x)\)
体積膨張率:\(γ\)
吸気流速\([L/sec]:V_{air}\)
吸気流速\([g/sec]:M_{air}\)
$$M_{air} [g/sec]=f(\frac{V_{air} [L/sec]}{γ})$$
膨張した分を割って理想状態に変換する必要がある。
その割る係数が体積膨張率\(γ\)となる。
体積\([L]\)と質量\([g]\)は\(mol\)を経由すると相互変換が可能なものである。
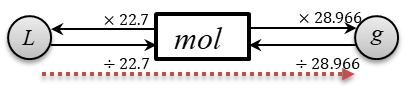
\(f(x)\)は空気の体積から質量に変換すれば良い関数なので以下となる。
\(1mol\)の標準体積:\(22.7[L]\)
空気の平均\(mol\)質量:\(28.966[g/mol]\)
$$f(x)=x[L/sec]×\frac{28.966[g/mol]}{22.7[L/mol]}$$
体積膨張率
あとは体積膨張率を求める。
ちなみにボイル・シャルルの法則は以下。
圧力:\(P\)
体積:\(V\)
絶対温度:\(T\)
定数(同一の物質であれば固定):\(k\)
$$\frac{P×V}{T}=k$$
ボイル=シャルルの法則(ボイルシャルルのほうそく、英: combined gas law)は、理想気体の体積と圧力、温度に関係する法則[1]。シャルルの法則、ボイルの法則、ゲイ=リュサックの法則を組み合わせたものである。この法則の公式的な発見者はおらず、すでに発見されていた法則を融合させたものである。これらの法則は、気体の圧力、体積、絶対温度のうち任意の2変数が、その他の変数を定数として置いた場合、互いに比例あるいは反比例することを示している。
Wikipediaより
ボイル・シャルルの法則を元に\(STP\)条件と現在の条件の比較式を作る
※\(V_{act} [L]\)が求めたい実体積。
左辺:\(1mol\)の体積が\(22.7[L]\)時の標準圧力と標準温度
右辺:現在の圧力と温度
$$\frac{100[kPa]×22.7[L]}{273.15[K]}=\frac{101.325[kPa]×V_{act}[L]}{292.00[K]}$$
上記の式を元に\(V_{act}\)を解く。
$$101.325[kPa]×V_{act}=\frac{100[kPa×22.8[L]×292.00[K]}{273.15[K]}$$
$$V_{act}=\frac{100[kPa]×22.7[L]×292.00[K]}{273.15[K]×101.325[kPa]}$$
$$V_{act}[L]≒23.9[L]$$
現在の大気温度、大気圧においての\(1mol\)の体積は\(23.9[L]\)となる。
欲しいのは体積膨張率であるため、\(1mol\)に於いての標準体積で割ることで求める。
\(1mol\)の標準体積:\(22.7[L]\)
体積膨張率\(γ\)
$$γ=\frac{V_{act}[L]}{22.7[L]}$$
$$γ≒\frac{23.9[L]}{22.7[L]}$$
$$γ≒1.052863436123348$$
これが現在の大気温度、大気圧においての体積膨張率となる。
演算誤差問題
ところが、\(V_{act}\)を算出した時にかなり丸めが発生している。
この丸め誤差は無視できない誤差である可能性が高い。
左辺:\(1mol\)の体積が\(22.7[L]\)時の標準圧力と標準温度
右辺:現在の圧力と温度
$$\frac{100[kPa]×22.7}{273.15[K]}=\frac{101.325[kPa]×V_{act}[L]}{292.00[K]}$$
左辺の\(1mol\)の標準体積\(22.7[L]\)を早々に右辺に移項すると以下になる。
$$\frac{100[kPa]}{273.15[K]}=\frac{101.325[kPa]×\displaystyle\frac{V_{act}}{22.7[L]}}{292.00[K]}$$
右辺に、体積膨張率を示す\(\displaystyle \frac{V_{act}}{22.7[L]}\)が現れるので、早々に体積膨張率\(γ\)と置き換える。
$$\frac{100[kPa]}{273.15[K]}=\frac{101.325[kPa]×γ}{292.00[K]}$$
$$γ=\frac{100[kPa]×292.00[K]}{273.15[K]×101.325[kPa]}$$
$$γ=1.0550305468829426$$
$$γ≒1.055$$
これにより丸め誤差を最小にすることができる。
変換関数
吸気流速\(V_{air} [L/sec]\) → 吸気流速\(M_{air} [g/sec]\)変換式は以下となる。
$$F(x)=f(\frac{x}{γ})$$
$$=\frac{x[L/sec]×28.966[g/mol]}{22.700[L]×1.055[-]}$$
$$=\frac{1.276035242290749[g/L]×x[L/sec]}{1.055[-]}$$
$$≒1.210[g/L]×x[L/sec]$$
$$=1.210x[g/sec]$$
まとめ
- 体積は圧力(気圧)、温度の影響を受けて変化する。
- 体積と質量の変換は\(mol\)を経由すると楽ができる。
- 演算回数が多いので、算出方法をある程度最適化しないと演算誤差が乗りやすくなる。
おまけ(外部環境が変化する場合)
今回に於いては定数にしているが、本来は外部環境が変化するため変数にすべき
よって、以下が実用的な式となる。
$$F(x,γ)=\frac{1.276[g/L]×x[L/sec]}{γ[-]}$$
実際のECU内の処理では「エアフロメータ電圧\([V]\)」と「大気圧\([kPa]\)」を入力としたMAPに突っこんで\(G_{air} [g/sec]\)をイキナリ導出する場合もあるが、これは上記物理値変換をMAP内の係数で吸収しただけの話となる。




コメント