MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第4章 その10【形式ニューロン⑧】
を書き直したもの。
形式ニューロン且つ総当たり法によるパラメータ特定のプログラム化
今回はMATLABで実現。
【再掲】処理フロー
今回から「形式ニューロン且つ総当たり法によるパラメータ特定のプログラム化」
まずは処理フローを再掲。
- 入力データセットの定義
- 出力データセットの定義
- パラメータ変数の定義(重み、バイアス)
- 学習率定義
- 重みとバイアスの総当たり計算(ループ)
- 重みとバイアスを使用して予測値を算出
- 損失の計算
- 損失の更新
- 最も損失が小さいパラメータの記憶
- 学習結果の表示
- 出力結果の確認
これをMATLABで実現する。
MATLABコード
MATLABコードは以下。
heaviside.m
function y = heaviside(x)
y = double(x >= 0);
end% データセットの入力
X = [0, 0; 0, 1; 1, 0; 1, 1];
% データセットの出力
Y = [0; 0; 0; 1];
% パラメータの初期値
W = zeros(2, 1); % 重み
b = 0; % バイアス
num_epochs = 10000; % 学習のエポック数
learning_rate = 0.1; % 学習率
min_loss = realmax;
learning_range = 4;
n=length(Y)
% 重みの総当たり計算
for w1 = -learning_range:learning_rate:learning_range
for w2 = -learning_range:learning_rate:learning_range
for b = -learning_range:learning_rate:learning_range
% フォワードプロパゲーション
Z = X * [w1; w2] + b; % 重みとバイアスを使用して予測値を計算
A=heaviside(Z); % ヘヴィサイド活性化関数を適用
% 損失の計算
loss = 1/n * sum((A - Y).^2); % 平均二乗誤差
% 最小損失の更新
if loss < min_loss
min_loss = loss;
best_w1 = w1;
best_w2 = w2;
best_b = b;
end
end
end
% ログの表示
fprintf('loss: %f\n', min_loss);
fprintf('weight: w1 = %f, w2 = %f\n', best_w1, best_w2);
fprintf('bias: b = %f\n', best_b);
end
% 最小損失の重みを更新
W = [best_w1; best_w2];
b = best_b;
% 学習結果の表示
fprintf('learning completed\n');
fprintf('weight: w1 = %f, w2 = %f\n', W(1), W(2));
fprintf('bias: b = %f\n', b);
% 出力結果確認
fprintf("X=")
disp(X)
fprintf("hatY=")
disp(heaviside(X*[W(1);W(2)]+b))
figure;
hold on;
scatter(X(Y == 0, 1), X(Y == 0, 2), 'filled', 'MarkerFaceColor', 'r');
scatter(X(Y == 1, 1), X(Y == 1, 2), 'filled', 'MarkerFaceColor', 'b');
x1 = [min(X(:, 1))-1 max(X(:, 1))+1];
x2 = -(W(1)*x1 + b) / W(2);
plot(x1, x2, 'k', 'LineWidth', 2);
xlim([-0.5 1.5]);
ylim([-0.5 1.5]);
title(sprintf('Loss: %.4f', loss));
legend('Class 0', 'Class 1', 'Decision Boundary');
grid on;
hold off;
処理結果
処理結果は以下。
X=
0 0
0 1
1 0
1 1
hatY=
0
0
0
1
W=
0.1000
0.1000
b=
-0.2000考察
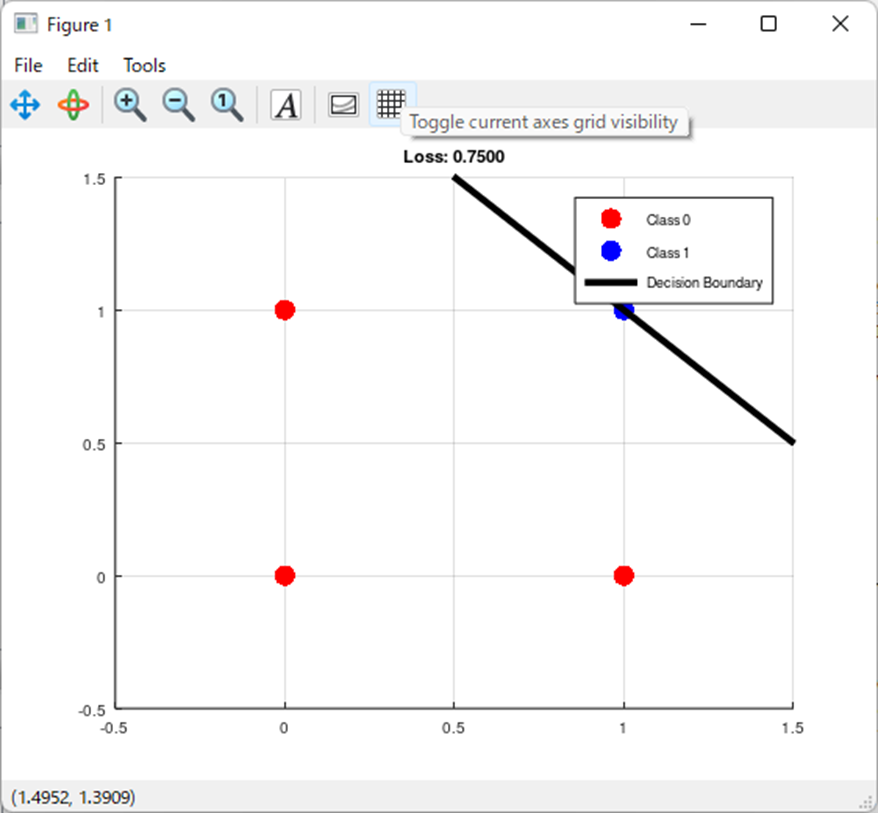
入力と出力の結果を見ると、
ちゃんとANDの真理値表になってる。
しかし、決定境界直線の位置が随分ギリギリのところになってしまっている。
これが形式ニューロンの欠点といえ、。
これを理由とした課題が形式ニューロンにあるため、ほぼ使われない面もある。
とりあえず、今回の結果として問題無いとする。
まとめ
- 形式ニューロンをMATLABで実現。
- ANDの真理値表と同じ結果が得らえれた。
- しかし、決定境界線はギリギリな感じ。
MATLAB、Python、Scilab、Julia比較ページはこちら





コメント