バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
形式ニューロンについての解説。
分類問題のHelloWorldに相当する話。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】形式ニューロンへ至る道

まずは、形式ニューロンへ至る道を再掲。
- ヘヴィサイド関数(済)
- 形式ニューロン(済)
- 分類問題のHelloWorld
- 誤差関数
- 決定境界直線
- 決定境界直線の特定方法
- 総当たり法による分類

分類問題のHelloWorldに相当する話。
HelloWorld

よくプログラムをする際に
標準出力方法を最初に学ぶことが多い。

「HelloWorld」とか出力するあれだね。

今回は、分類問題の於けるHelloWorld相当の話になる。
と言っても、「HelloWorld」という文字列を表示するわけでは無く、
最も基本的且つ最もシンプルな話。という意味合いだけど。

最初はシンプルに限るよね。
難しい話されてもわからんし。
分類問題のHelloWorld

分類問題の於けるHelloWorldは、
ANDゲートになる。

ANDゲートって、2入力あって、
両方が1なら1、どちらかが0だったら0になる。
ってやつだよね?

そうそう。
真理値表で表現するとこうなる。
ANDゲートの真理値表
| \(x_1\) | \(x_2\) | \(y\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |

まぁ、これはわかる。
2入力1出力の形式ニューロン

この際のANDゲートを、形式ニューロンで表現したい。
この場合の形式ニューロンは
2入力1出力の構成になる。
概念図で示すと以下になる。
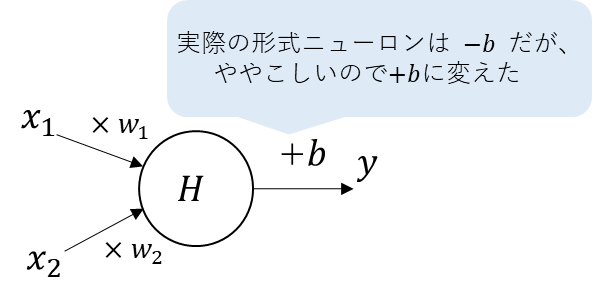

形式ニューロンのバイアスは、本来であれば\(-b\)で表現されるが、
話をシンプルにするために\(+b\)に表現しなおしている。

毎回、マイナスを意識するのもめんどうだもんね。

そして、これを数式で表現すると以下になる。
\(
y=H\Bigg(
\begin{bmatrix}
w_1&w_2&b
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
1
\end{bmatrix}
\Bigg)
\)

前回の概念図、数式からすると、確かにこうなるね。

この構成をもって、適切な\(w_1,w_2,b\)を探すことが、分類問題を解く。
ということになる。
まとめ

まとめだよ。
- 分類問題のHelloWorld総統はANDゲート。
- ANDゲートを形式ニューロンで実現するための構成を説明。
- 2入力1出力の構成になる。
バックナンバーはこちら。




コメント