バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
今回から形式ニューロンについての解説に突入。
まずはロードマップの提示から。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
形式ニューロンに至る道

まずは形式ニューロンってのをやるんだっけ?

そうそう。

これも、単に形式ニューロンだけの説明で終わる感じじゃないような気がする。

中々察しが良いね。
複数の知識の組み合わせで成立すると思った方が良いな。

じゃー、恒例のロードマップをよろしくー

おおよそ以下の手順で説明していく。
- ヘヴィサイド関数
- 形式ニューロン
- 分類問題のHelloWorld
- 誤差関数
- 決定境界直線
- 決定境界直線の特定方法
- 総当たり法による分類

予想以上に盛沢山じゃねぇか・・・。

まぁ、一つ一つはシンプル・・・なはず・・・。

(シンプルじゃないのもあるって雰囲気だな・・・。)
ヘヴィサイド関数

まずはヘヴィサイド関数。
これが形式ニューロンの性格を顕著に表すものと言って良いだろう。

どんな関数なの?

まずはWikipediaから引用。
ヘヴィサイドの階段関数(、英: Heaviside step function)は、正負の引数に対しそれぞれ 1, 0 を返す階段関数である。名称はオリヴァー・ヘヴィサイドにちなむ。ヘヴィサイド関数と呼ばれることもある。通常、H(x) や Y(x) などで表されることが多い。
Wikipediaより(https://ja.wikipedia.org/wiki/%E3%83%98%E3%83%B4%E3%82%A3%E3%82%B5%E3%82%A4%E3%83%89%E3%81%AE%E9%9A%8E%E6%AE%B5%E9%96%A2%E6%95%B0)

これだけ見てもわからん・・・。

グラフにするとこんな感じだな。
連続系を非連続系に変換する関数の最もシンプルなものだ。
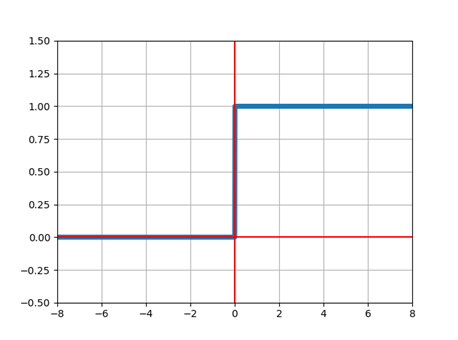

正の入力だと1、負の入力だと0ってことかな?

そうそう。
この関数の性格を利用すると、
もやっとしたものをYes/Noに変換できるとと思っておけば良いだろう。

そういう表現だと分かり易いな。
まとめ

まとめだよ。
- 形式ニューロンを把握するためのロードマップを提示。
- ヘヴィサイド関数を説明。
- とりあえず、もやっとしたものをYes/Noに変換できるとと思っておけばOK。
バックナンバーはこちら。




コメント