バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia3-backnumber/
はじめに
アフィン変換の拡張と言われている射影変換の話。
射影変換の理屈について
「3次元空間を地面平面に落とし込む」について
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】射影変換の理屈の因果関係

まずは大まかな流れを再掲
- 大まかな理屈(済)
- 大まかな理屈を座標変換で説明(済)
- 基本ベクトルと基底ベクトル(済)
- 元画像平面を3次元空間で表現(済)
- 3次元空間を地面平面に落とし込む
- 一連の座標変換まとめ
- 方程式の変形
- 行列表現
- アフィン変換との関係性
- 係数の求め方
- 係数の求め方(行列表現)
- 射影変換の処理の流れ

「元画像平面を3次元空間で表現」というところまで終わっている。
3次元空間を地面平面に落とし込む

今回は3次元平面に浮かせた元画像平面を
地面平面に落とし込む場合の話。
まぁ、地面平面の落とす、つまりこれが射影ってことだな。

確かに、影を落とす感じはあるね。

画像としてはこれを見るとわかるだろう。
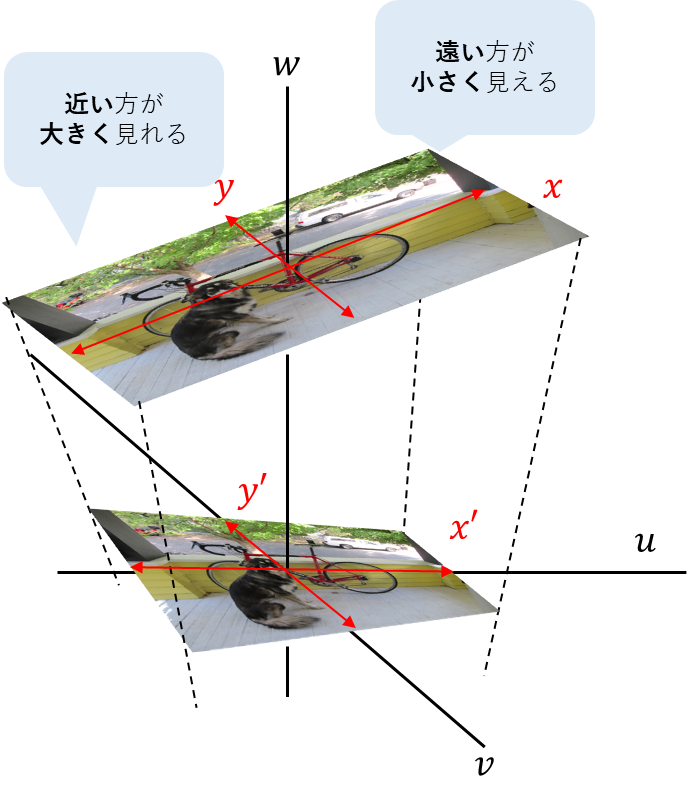

確かに、影を落とす感じはあるね。

考え方はシンプル。
まず、\(x\prime\)と\(u\)、\(y\prime\)と\(v\)は間違いなく相関性は強い。
ここに対して高さ\(w\)の補正を掛ける。
つまり、「地面からの距離が離れるほど小さく見える」を数式で再現できればOK。
これらを加味した式は以下になる。
\(
\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle x\prime=\frac{u}{w} \\
\displaystyle y\prime=\frac{v}{w}
\end{array}
\right.
\end{eqnarray}
\)

あ、これだけでいいのか。
言われてみれば、納得だ。

台形に利くのが\(w\)だね。
これがアフィン変換にはない概念を生み出している。

たしかに、\(w\)が無かったら、
移動、回転、伸縮くらいしかできなそうだもんね。
まとめ

まとめだよ。
- 「3次元空間を地面平面に落とし込む」
- 高さwのパラメータが重要で、これの影響でアフィン変換ではできなかった台形の対応が可能となる。
バックナンバーはこちら。




コメント