バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia3-backnumber/
はじめに
アフィン変換の拡張と言われている射影変換の話。
そもそも射影変換のできることは?
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
射影変換でできること

射影変換がアフィン変換の拡張と言われてはいるが、
概念上はことなるもので、
結果的な数式が似ることと、
アフィン行列を元に射影変換をするとアフィン変換が実現できてしまうところから
「アフィン変換の拡張」と言われてるらしい。
ってところまではわかったけど、
結局、射影変換って何ができるの?

アフィン変換相当ができることに加えて、
台形変換ができるのが特徴になるね。

台形変換?

こんなことができる。


なんかス〇ーウォーズみてぇになってるな。
現実世界での利用方法

あとは、自動車の全方位モニタを実現する技術として
射影変換が使用されてるな。

真上から見たような感じするアレか。
なんか、すごいことをやってそうだな・・・。

まぁ、細かい部分を上げると大変なことをやっていると思うが、
横方向に撮影したものを、射影変換を用いて、台形上に変換して、
一見すると上から見たような状態にしてるだけだな。


あとは、名刺の取り込みアプリとかだな。

あー、こういうやつだね。
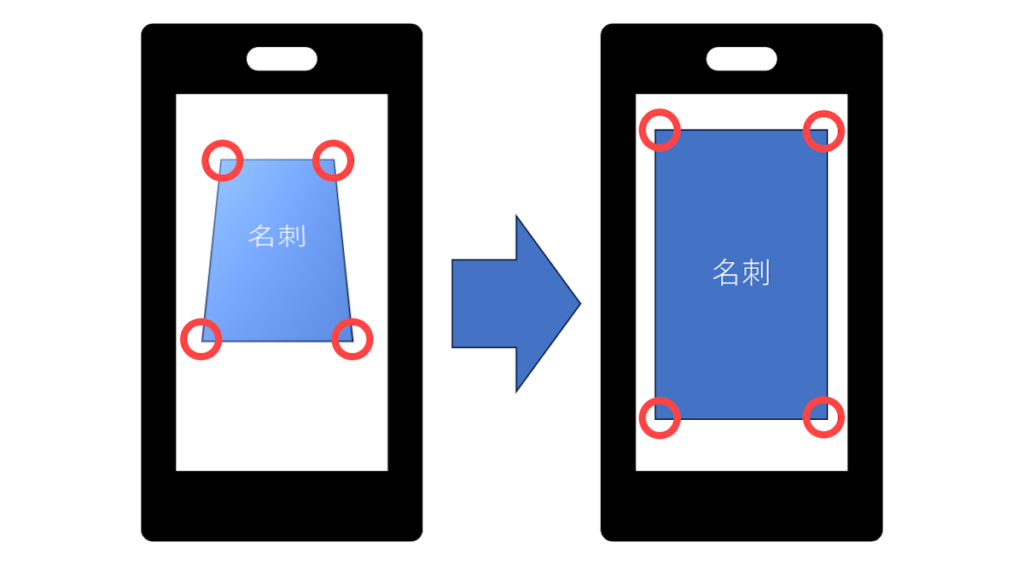
結局どんな変換をしているのか?

でも、全方位モニタは、長方形を台形へ、
名刺取り込みは台形を長方形へ変換。
結局、射影変換はどっちをやってくれるんだ?

両方だな。


当然、台形から台形への変換も出来る。
要は、四隅の頂点をどこの座標に移動させるかと言う意味ではどれも一緒なんだよね。

なるほど。
四隅の点に着目するのか。

まぁ、これを実現する上での理屈があるのだが、それは次回。
まとめ

まとめだよ。
- 射影変換で出来ることを確認。
- 現実世界での利用方法を紹介。
- 射影変換は四隅の点をどこに移動させるかという変換。
- 長方形から台形、台形から長方形、台形から台形。
バックナンバーはこちら。




コメント