バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia3-backnumber/
はじめに
アフィン変換の続き。
各種アフィン変換とアフィン行列について。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
各種アフィン変換とアフィン行列

今回は各種アフィン変換をする場合のアフィン行列をどうするかって話だね。

そうそう。
確認するのは以下になる。
- 伸縮
- 移動
- 回転
- 剪断

この名称はアフィン変換の最初の方でも出てきたね。

基本はこの4つの組み合わせで処理することになる。
伸縮

まずは伸縮。
\(x\)軸方向に引き延ばす場合は、\(x\prime\)が\(x\)に係数が掛かればOK。
\(y\)軸も考え方は一緒だな。


座標変換という考え方に則れば当然か。
移動

次は移動。
これは\(x\)軸、または\(y\)軸の方向にバイアスを載せればOK。
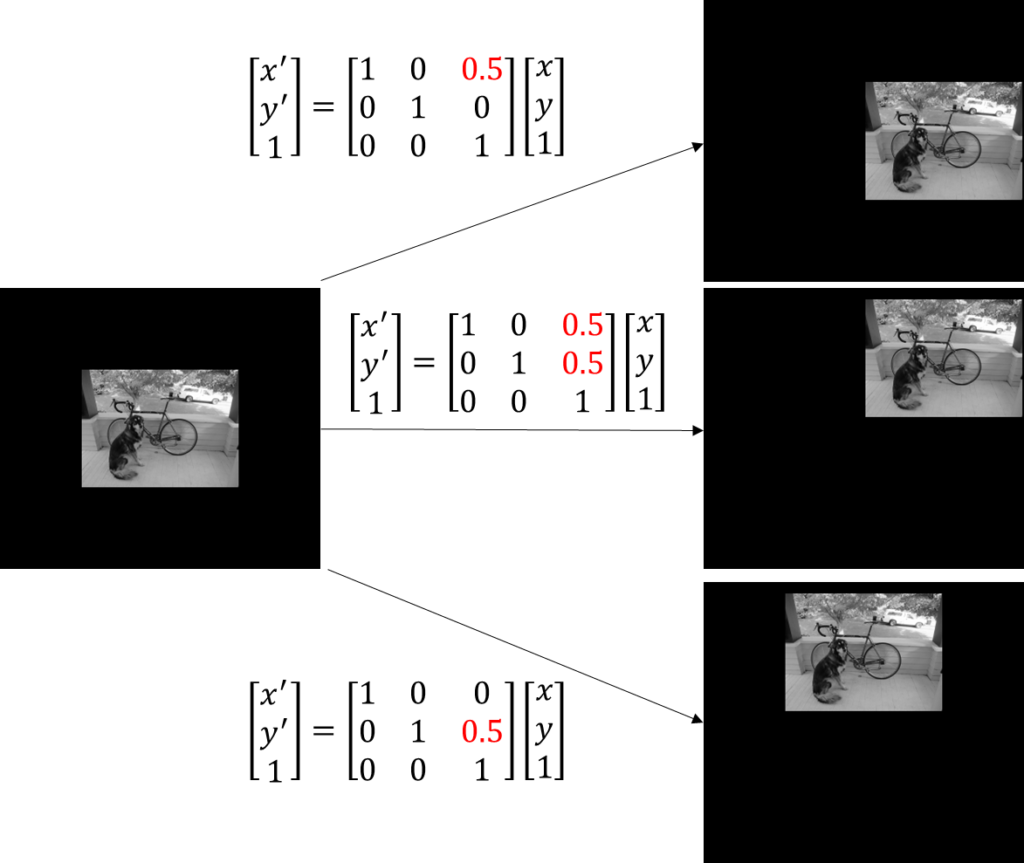

これも落ち着いてみれば当然の話か。
回転

ここら辺から少しややこしくなる。
回転だ。
回転行列を使って、回転後の座標を推定する。
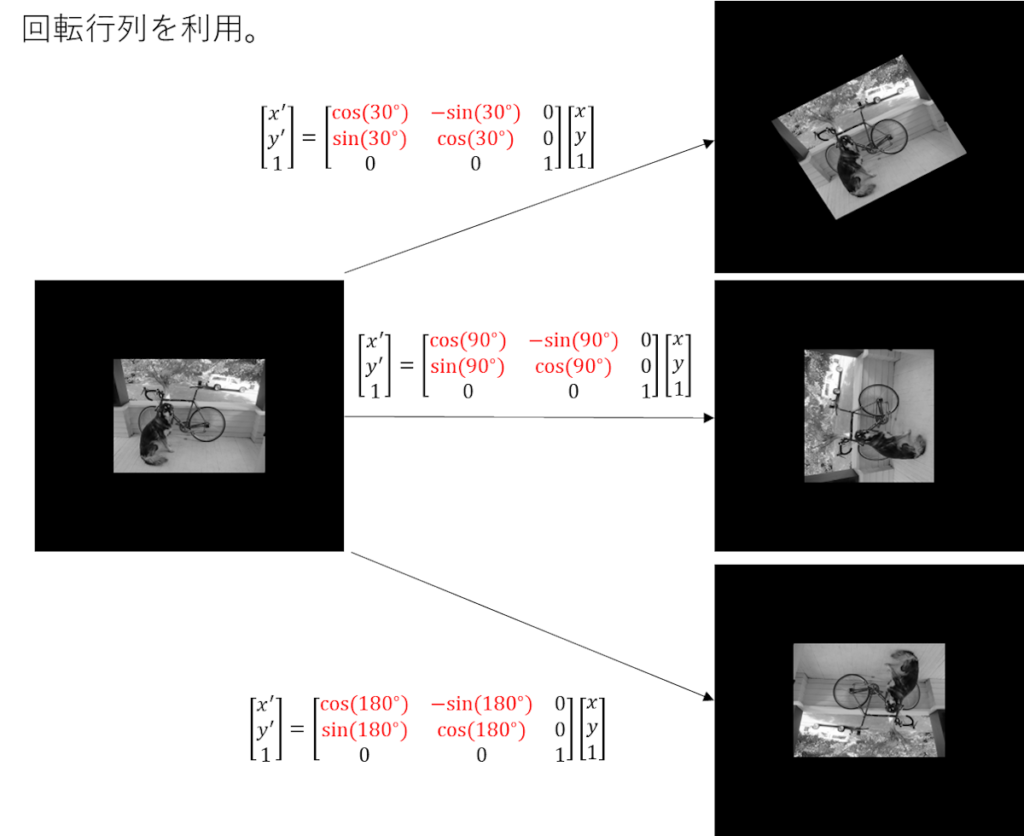

回転行列がわからん・・・。

これもそれほど複雑ではないが、別途説明しよう。
剪断

次は剪断。
これも若干ややこしい。
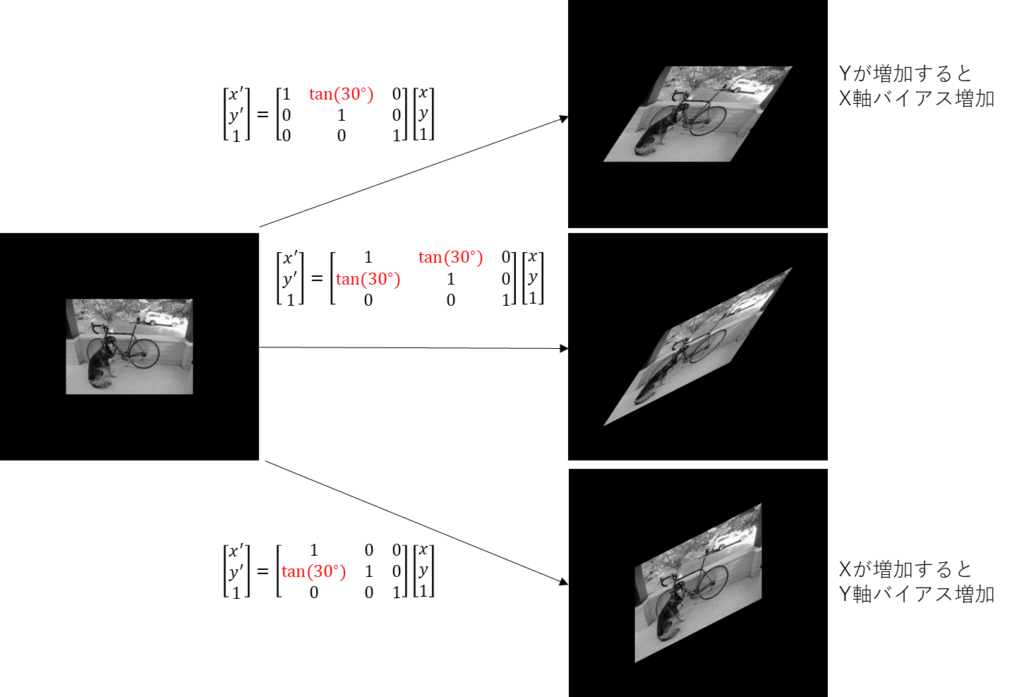

\(\tan(\theta)\)とか入ってて意味わからん・・・。

これは冷静に考えると分かるのだが、
\(\tan(\theta)\)は角度\(\theta\)時の\(x\)と\(y\)の比率だ。
\(\tan(30^{\circ})\)
つまり、\(y\)が大きくなるほど、\(x\prime\)は\(1/\sqrt{3}\times y\)分ずれていく。

あー、そのずれた結果がこの斜めった画像ってことか。

そうそう。
というわけで?

じゃー、今度こそ実際にプログラm

ちょい待ち!

まだなんかあるんかー!?

さっきの回転行列の話がまだ終わってない。

そういやあったな。

それを次回説明してから、
その後にプログラムを作成についての話に入る。
まとめ

まとめだよ。
- 各種アフィン変換とアフィン行列の説明。
- 伸縮、移動、回転、剪断。
- 回転は回転行列を使ってるので少しわかりにくい。
- よって、別途説明。
バックナンバーはこちら。




コメント