バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia3-backnumber/
はじめに
アフィン変換の続き。
だが、ちょっと余談にそれる
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
余談

とりあえず、キャンバス拡張も出来たところでアフィン変換に突入かな。

その前に少し余談を入れておこう。

余談?

以前やった畳み込み演算と今回のアフィン変換は
畳み込みニューラルネットワークと関連してるって話。

畳み込み演算は、まぁ名前的に関係性はありそうだけど、
アフィン変換は関係しているイメージは無いなぁ。

当然、アフィン変換自体がそのまま関係しているわけじゃないけど、
無関係というわけでもない。
その点を少し知っておこうって程度だ。
畳み込みニューラルネットワークの構造

まず、畳み込みニューラルネットワークの基本的な構造を示そう。
当然、さまざまネットワークがあるから、今回の説明に於いての前提としてこう解釈する
って意味合いだ。
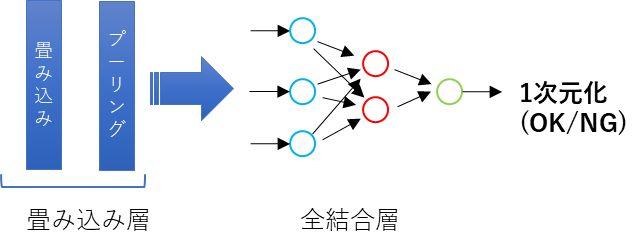

まぁ、あんまり詳しくないけど、
これが基本的な構造ってのはわかる。
畳み込み層

左側の畳み込み層。
厳密には畳み込み層とプーリング層がふくまれるわけだが、
これがやっているのはおおよそ以下。
- 輪郭検出
- 次元削減
- 抽象化
画像で示すとこんな感じだ。


確かに畳み込み演算がベースになってるよね。
ニューロン

次に全結合層だが、その前に
ニューロンについて確認する。
ニューロンは以下で表現される。
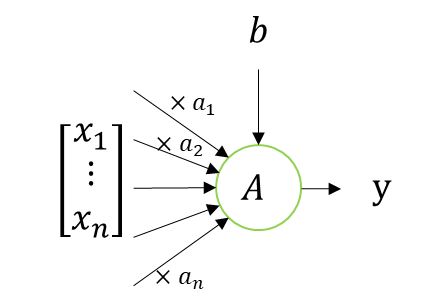

これも良く見るね。

このニューロンの演算って実は、\(x\)ベクトルと重みの\(a\)ベクトルの内積と解釈できる。
数式を出すとこうなる。
\(
y=A\Bigg(
\begin{bmatrix}
a_1 & \dots & a_n & b
\end{bmatrix}
\begin{bmatrix}
x_1 \\
\vdots \\
x_n \\
1
\end{bmatrix}
\Bigg)
\)

確かに、計算としては一緒だ!

ニューロン一個だとこんな感じだが、
これが複数になると・・・。

(ゴクリ・・・。)

これについては次回説明!

(地味に話が長くなるんだな・・・。)
まとめ

まとめだよ。
- 余談として畳み込みニューラルネットワークと畳み込み演算、アフィン変換の関連性を説明。
- 畳み込み層と畳み込み演算は割とそのまんまでわかりやすい。
- 全結合層の前にニューロン1個の演算を数式で表現。
バックナンバーはこちら。




コメント