はじめに
LAF(全領域空燃比)センサ特性をPythonを用いて同定する。
アルゴリズムは最小二乗法を使用。
尚、本記事で出てくるLAFセンサ特性は実際の物とは異なり、本物っぽい偽物を使っている。
※ MATLAB版はこちら。
https://www.simulationroom999.com/blog/matlab-laf-sensor-characteristic/
MATLAB,Python,Scilab比較ページはこちら。
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
発端
排ガス規制対応のため、A/Fを計測することになったのだが、以下の課題有り。
- LAFセンサの物理値(A/F)そのものがECUからゲットできない。
- (ECU側で物理値変換していない?)
- LAFセンサの特性はリニアと思いきや、それほどリニアではない。
- LAF(Linear Air Fuel ratio)という名前がついている割には全然リニアじゃない
- 複数のセンサ特性が存在。
特性テーブルはあるので、線形補間型のテーブル変換でも良いが、使用している計測器の変換テーブル点数がそれほど多くなく・・・。つまり点数が全然足りない。。。
というわけで、Pythonを使ってLAFセンサの特性を2次関数で同定してみて、なんとか辻褄を合わせる。
※ 2次関数の変換式を挟むことはできる。
とりあえず、LAFセンサ特性は以下。
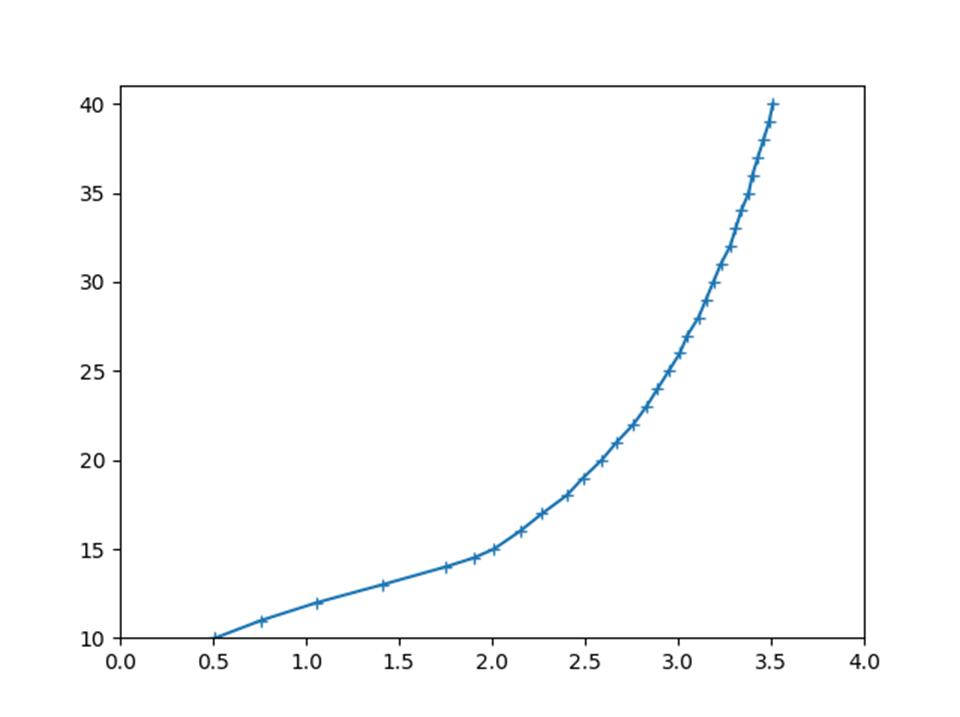
結果
いい感じにできた。
しかも、異なる特性が来ても割と簡単に同定できるので、この業務に関しては怖いもの無し!
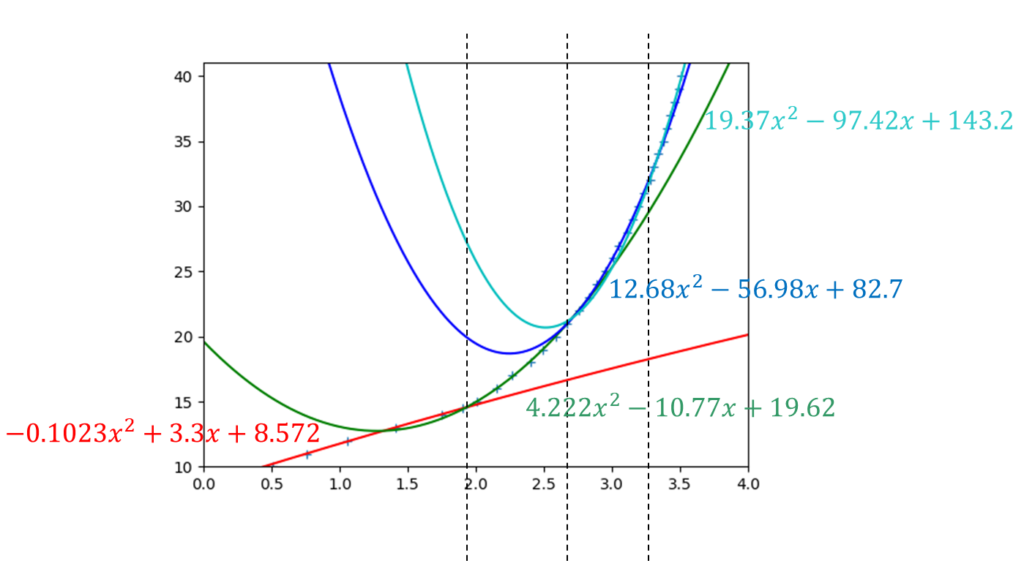
複数の波形を区間別に使用する。
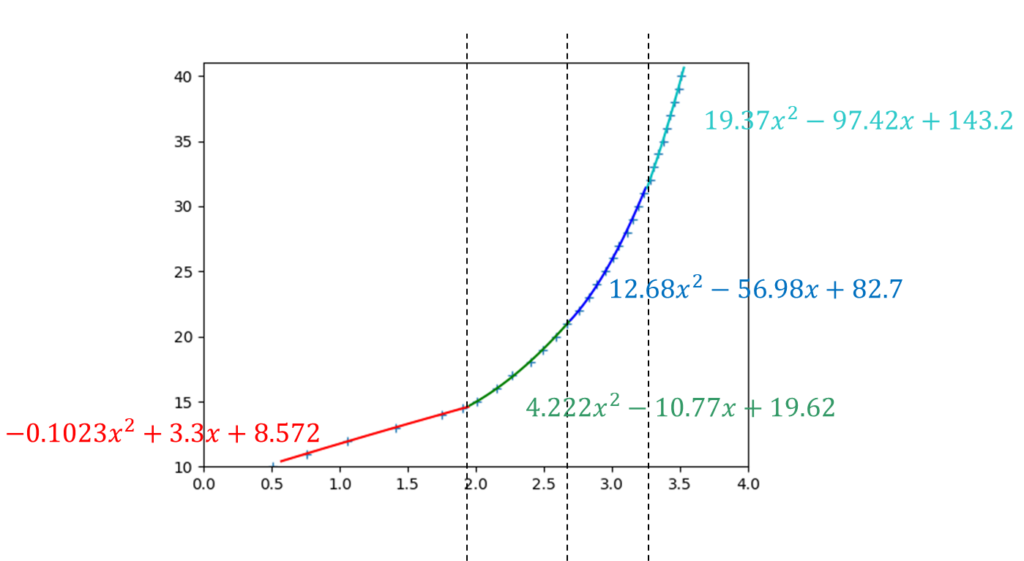
各波形を、使用区間だけ表示すると、こんな感じでかなりぴったり。
最小二乗法とは
最小二乗法(さいしょうにじょうほう、さいしょうじじょうほう;最小自乗法とも書く、英: least squares method)は、測定で得られた数値の組を、適当なモデルから想定される1次関数、対数曲線など特定の関数を用いて近似するときに、想定する関数が測定値に対してよい近似となるように、残差の二乗和を最小とするような係数を決定する方法、あるいはそのような方法によって近似を行うことである。
Wikipediaより
要は、基本モデルとなる関数(n次関数)を定義し、各係数を調整していったときに、各計測点との誤差の合計が最も少なくなる係数を真とする同定手法。
誤差はそのままだとプラス方向、マイナス方向で合計すると相殺してしまう。
よって、2乗して、符号の影響を受けない状態で評価する。
なので、「最小二乗法」という名前になる。
今回のLAFセンサ特性に対して1次関数で最小二乗法を適用すると、以下の感じになる。
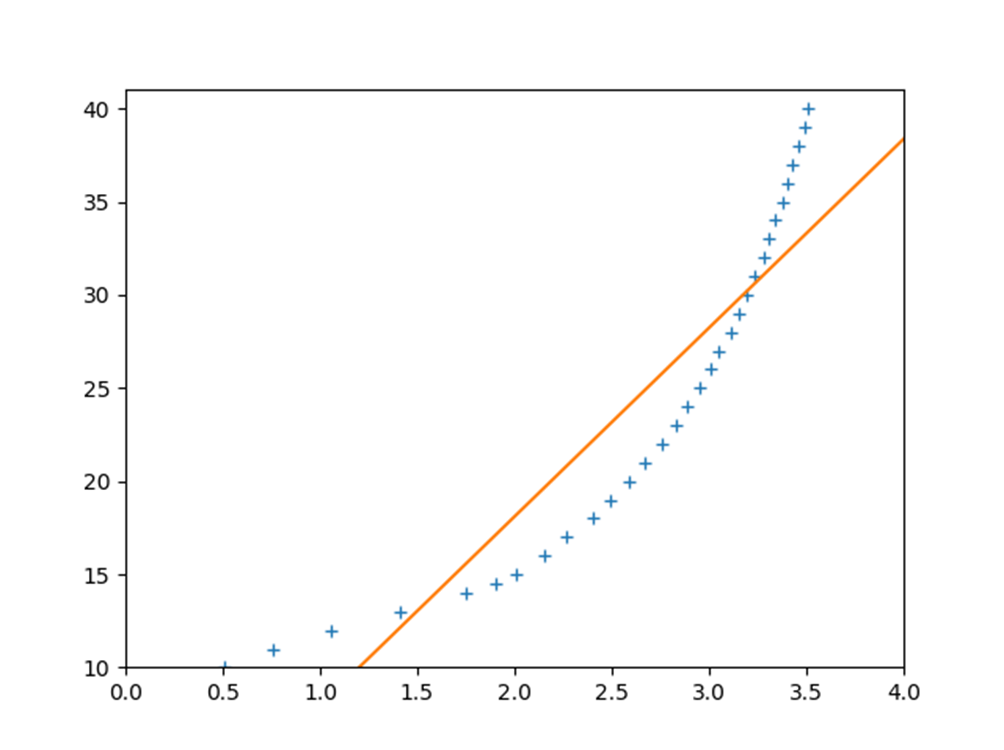
Pythonによる最小二乗法
NumPyのpolyfitとpoly1dを使用すれば一撃のように見える。
実験コード。
import numpy as np
import matplotlib.pyplot as plt
x = np.array([0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49, 2.59, 2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19, 3.23, 3.28, 3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51])
y = np.array([10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40])
coef = np.polyfit(x, y, 2) # 最小二乗法で得られた2次関数の各係数
print("各係数", end=':')
print(coef)
quad_func = np.poly1d(coef) # 2次関数の各係数から2次関数を生成
print("関数:")
print(quad_func)
xp = np.linspace(0, 4, 400) # 同定した2次関数のx軸を生成
plt.plot(x, y, '+', \
xp, quad_func(xp), '-' )
plt.ylim(10,41)
plt.xlim(0,4)
plt.show()
結果
各係数:[ 4.89519634 -11.32444228 17.09391213]
関数:
2
4.895 x - 11.32 x + 17.09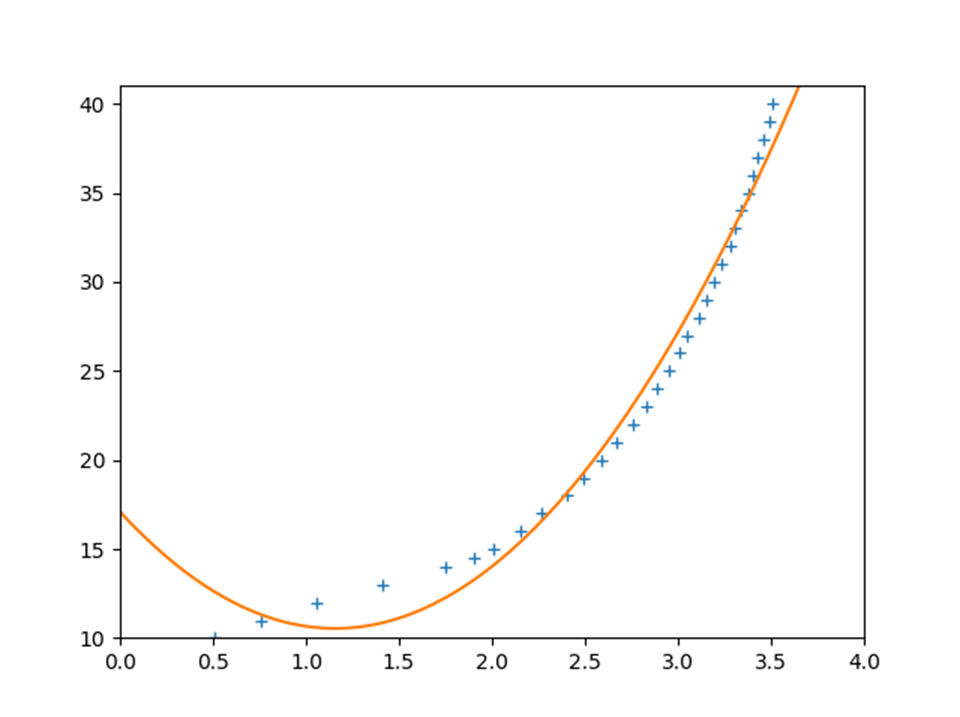
案の定、2次関数では同定しきれない。
感覚的に異なる特性っぽいところを分割する
ここで人間の感覚で大雑把に分割する。
別に悪いことではない。
機械が苦手なところを人間がやって、人間が苦手なところを機械にやってもらえれば良い。
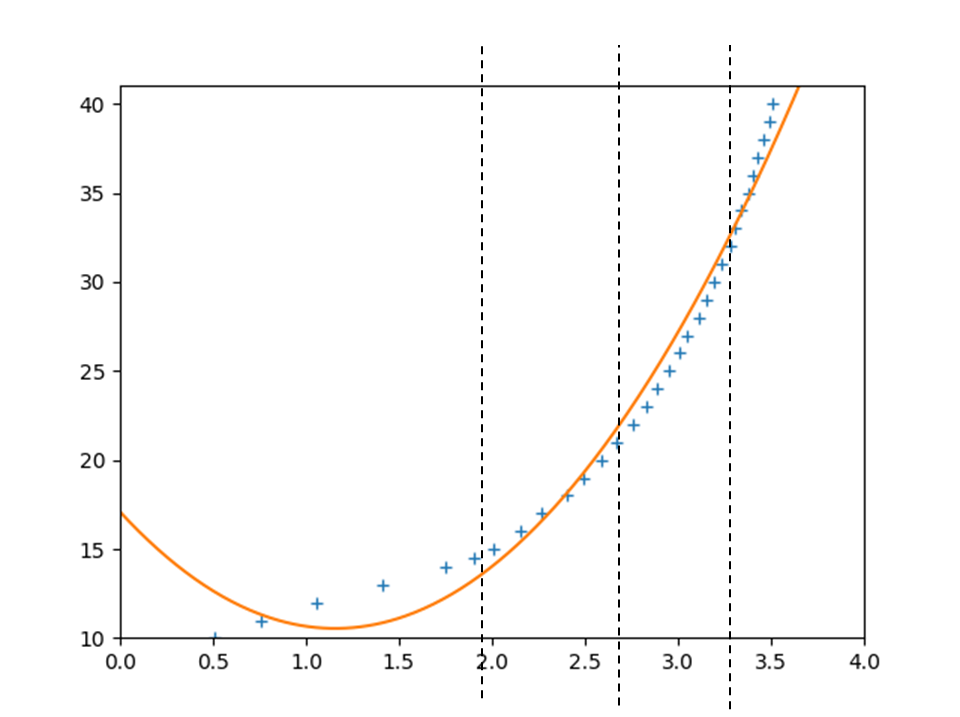
4分割で最小二乗法
実験コード
import numpy as np
import matplotlib.pyplot as plt
x = np.array([0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49, 2.59, 2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19, 3.23, 3.28, 3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51])
y = np.array([10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40])
# 第1区間
x1 = x[1:6]
y1 = y[1:6]
coef1 = np.polyfit(x1, y1, 2) # 最小二乗法で得られた2次関数の各係数
print("第1区間各係数", end=':')
print(coef1)
quad_func1 = np.poly1d(coef1) # 2次関数の各係数から2次関数を生成
print("第1区間関数:")
print(quad_func1)
# 第2区間
x2 = x[6:13]
y2 = y[6:13]
coef2 = np.polyfit(x2, y2, 2) # 最小二乗法で得られた2次関数の各係数
print("第2区間各係数", end=':')
print(coef2)
quad_func2 = np.poly1d(coef2) # 2次関数の各係数から2次関数を生成
print("第2区間関数:")
print(quad_func2)
# 第3区間
x3 = x[13:23]
y3 = y[13:23]
coef3 = np.polyfit(x3, y3, 2) # 最小二乗法で得られた2次関数の各係数
print("第3区間各係数", end=':')
print(coef3)
quad_func3 = np.poly1d(coef3) # 2次関数の各係数から2次関数を生成
print("第3区間関数:")
print(quad_func3)
# 第4区間
x4 = x[23:32]
y4 = y[23:32]
coef4 = np.polyfit(x4, y4, 2) # 最小二乗法で得られた2次関数の各係数
print("第3区間各係数", end=':')
print(coef4)
quad_func4 = np.poly1d(coef4) # 2次関数の各係数から2次関数を生成
print("第3区間関数:")
print(quad_func4)
xp = np.linspace(0, 4, 400) # 同定した2次関数のx軸を生成
#plt.plot(x, y, '+', \
# xp[57:195], quad_func1(xp[57:195]), '-r', \
# xp[195:269], quad_func2(xp[195:269]), '-g', \
# xp[269:325], quad_func3(xp[269:325]), '-b', \
# xp[325:353], quad_func4(xp[325:353]), '-c' )
plt.plot(x, y, '+', \
xp, quad_func1(xp), '-r', \
xp, quad_func2(xp), '-g', \
xp, quad_func3(xp), '-b', \
xp, quad_func4(xp), '-c' )
plt.ylim(10,41)
plt.xlim(0,4)
plt.show()
結果
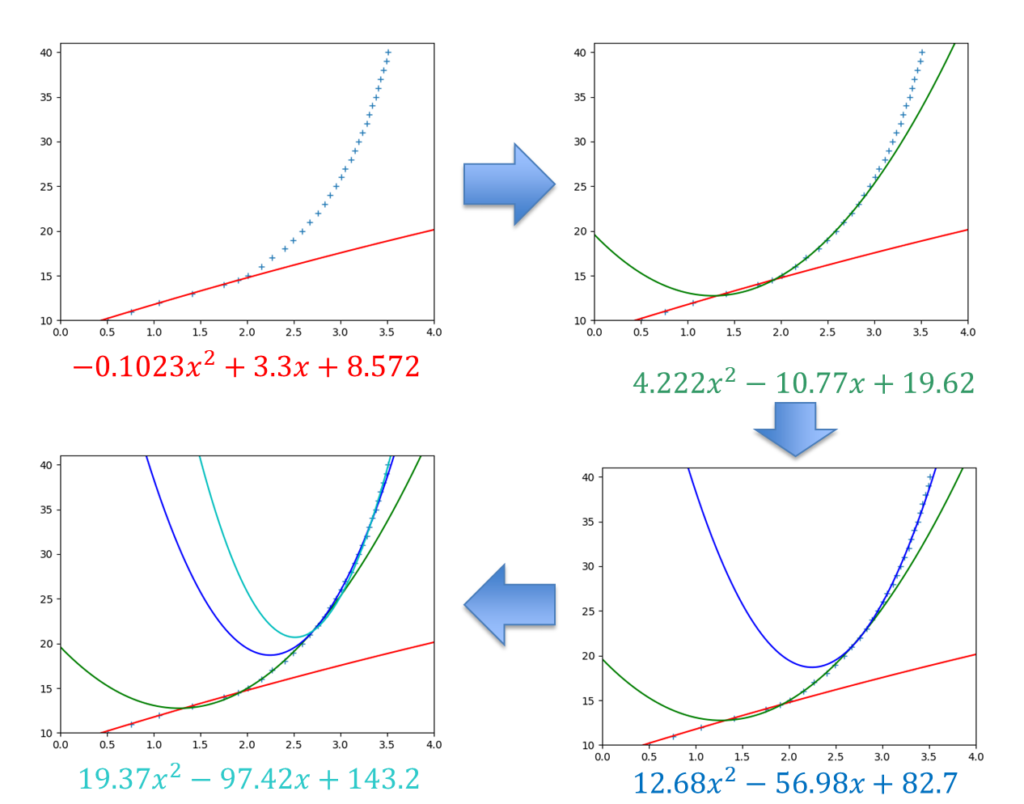
第1区間各係数:[-0.1023436 3.29971967 8.57167853]
第1区間関数:
2
-0.1023 x + 3.3 x + 8.572
第2区間各係数:[ 4.22152332 -10.76839825 19.61636121]
第2区間関数:
2
4.222 x - 10.77 x + 19.62
第3区間各係数:[ 12.68166941 -56.98425059 82.70467471]
第3区間関数:
2
12.68 x - 56.98 x + 82.7
第3区間各係数:[ 19.37359757 -97.41774436 143.15132863]
第3区間関数:
2
19.37 x - 97.42 x + 143.2
まとめ
- 特性テーブルをそのまま線形補間の変換テーブルに入れても良いが、何かしらの関数で同定できないか検討してみるのも良い。
- 計測器の都合で変換テーブルが使えなかったり、変換点数が限られていることがある。
- 大雑把な切り分けは人間の方が得意。
- 細かい調整や大量の演算は機械が得意。
- 機械と人間の共創が最大効率への道。
おまけ(7次関数で同定してみた)
実験コード
import numpy as np
import matplotlib.pyplot as plt
x = np.array([0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49, 2.59, 2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19, 3.23, 3.28, 3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51])
y = np.array([10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40])
coef = np.polyfit(x, y, 7) # 最小二乗法で得られた7次関数の各係数
print("各係数", end=':')
print(coef)
seven_func = np.poly1d(coef) # 各係数から7次関数を生成
print("関数:")
print(seven_func)
xp = np.linspace(0, 4, 400) # 同定した7次関数のx軸を生成
plt.plot(x, y, '+', \
xp, seven_func(xp), '-' )
plt.ylim(10,41)
plt.xlim(0,4)
plt.show()
結果
各係数:[ -0.07458869 1.39872766 -9.89915298 35.19248315 -66.72474712
66.3076464 -28.31200924 13.98702906]
関数:
7 6 5 4 3 2
-0.07459 x + 1.399 x - 9.899 x + 35.19 x - 66.72 x + 66.31 x - 28.31 x + 13.99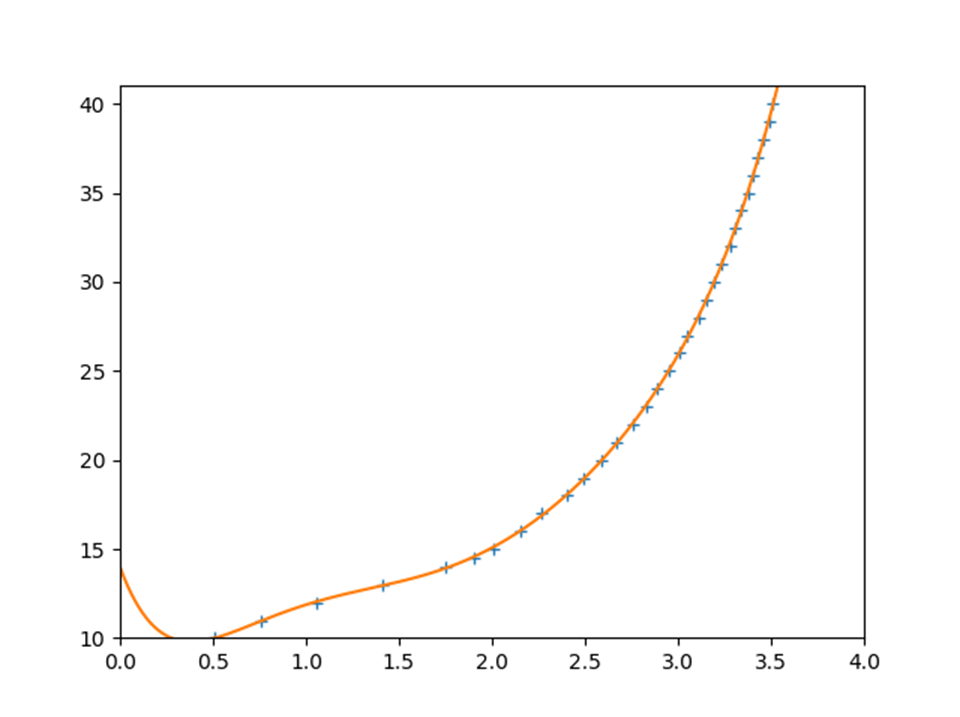
\(-0.07459x^7 + 1.399x^6- 9.899x^5+ 35.19x^4\)
\(- 66.72x^3+ 66.31x^2- 28.31 x + 13.99\)
7次関数で同定すると0近傍に変なしっぽが出るが、かなりいい感じで同定できる。
7次関数が許容できる環境であれば、これでも良い。
※ MATLAB版はこちら





コメント