【入門】非極大値抑制【数値計算】

MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/

【入門】MATLAB,Python,Scilab,Julia使い方比較【数値計算プログラム】

MATLAB,Python,Scilab,Juliaを比較。基本的な計算、ベクトル行列演算、グラフ(波形)表示、伝達関数、画像取り込み、最小二乗法を元に比較しています。それぞれツールの特性が理解できれば使い分けも移行も難しくは無いでしょう。似ている部分も多いので私の場合はそれを利用するして実験の幅を広げています。

www.simulationroom999.com

2020.04.12

はじめに

MATLAB,Python,Scilab,Julia比較 第3章【バックナンバー】

はじめに MATLAB,Python,Scilab,Julia比較するシリーズの第3章。 第2章では回帰関連の話がメインだった。 第3章は画像処理関連の話がメインとなる。基本的には以下の流れとなる。 画像の読み込み、保存 グレースケール 畳...

www.simulationroom999.com

2024.01.09

の、
MATLAB,Python,Scilab,Julia比較 第3章 その36【非極大値抑制①】
MATLAB,Python,Scilab,Julia比較 第3章 その37【非極大値抑制②】
MATLAB,Python,Scilab,Julia比較 第3章 その38【非極大値抑制③】
MATLAB,Python,Scilab,Julia比較 第3章 その39【非極大値抑制④】
MATLAB,Python,Scilab,Julia比較 第3章 その40【非極大値抑制⑤】

を書き直したもの。

非極大値抑制なるものの説明を以下の流れで説明。

エッジ検出をもっとシビアに！

前回までの話で、Sobelフィルタを用いてエッジ検出ができるわかったと思う。

が、
エッジの白い線が、細かったり、太かったりとマチマチ。
これは微分した結果なので当然と言えば当然。
実際は純粋な一本線みたいな感じで検出できる方が理想的ではある。

では、実際にそのようなことが可能なのか？

結論としては可能。
しかも、やることとしてはそれほど難しくはない。
(若干、理屈がややこしいとかはあるかもしれないが)

どうなっていたら良いのか。

実際どうなるかを先に説明しておく。

元画像

Sobelフィルタ実施

某処理実施

こんな感じで一本線、というかエッジが1ピクセルの幅で表現される。

何をしたのか？

これは非極大値抑制という処理を施したもの。
Non-maximum suppressionとも呼ばれる。

YOLOのような物体検出器でも同様の用語が出てくるが、それとは別物。
物体検出器の方は複数のバウンディングボックス候補のうち最も正しいものだけを残す機能。
広義で同一の概念とは言えるかもしれないが。

機能も名前の通りで、
「極大値じゃないものを抑制」する。
つまり、極大値だけをピンポイントで残す手法になる。

この手法については以下の順番で説明していく。

非極大値抑制の大雑把な雰囲気

名称からおおよそのイメージはできているかもしれないが、
一応、図解しておく。

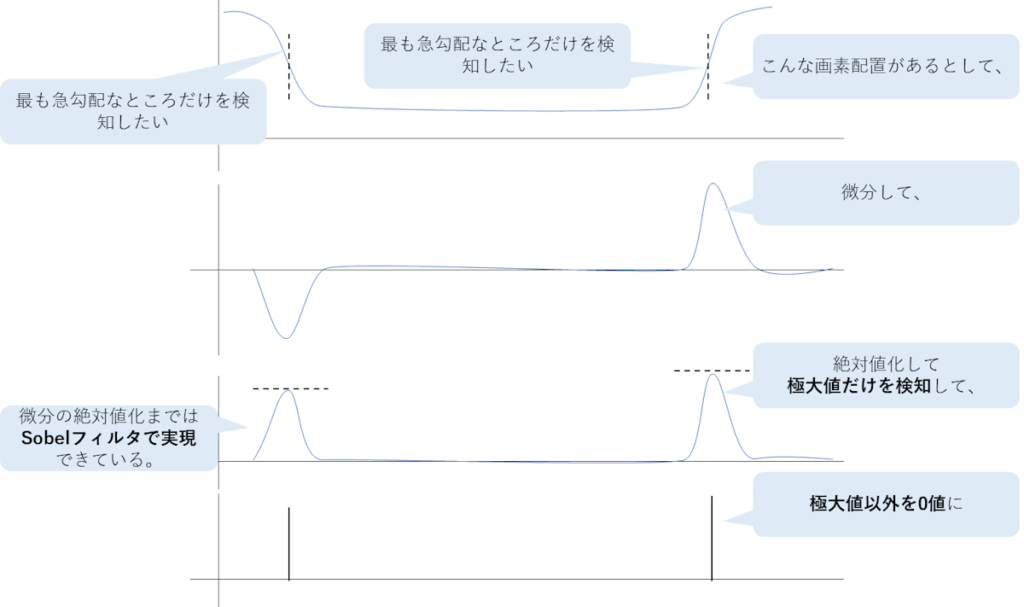
実は、上から3段目のところまではSobelフィルタで実現済み。
よって、最後の1段を実現すればOK。
つまり、Sobelフィルタだけでいいところまでは来てる。

2次元平面に実施する場合の考え方

と、まぁ、1次元でみるとシンプルは話ではあるのだが、
画像自体は2次元平面。
もう少し考える必要がある。

これも簡単に図解しておく。

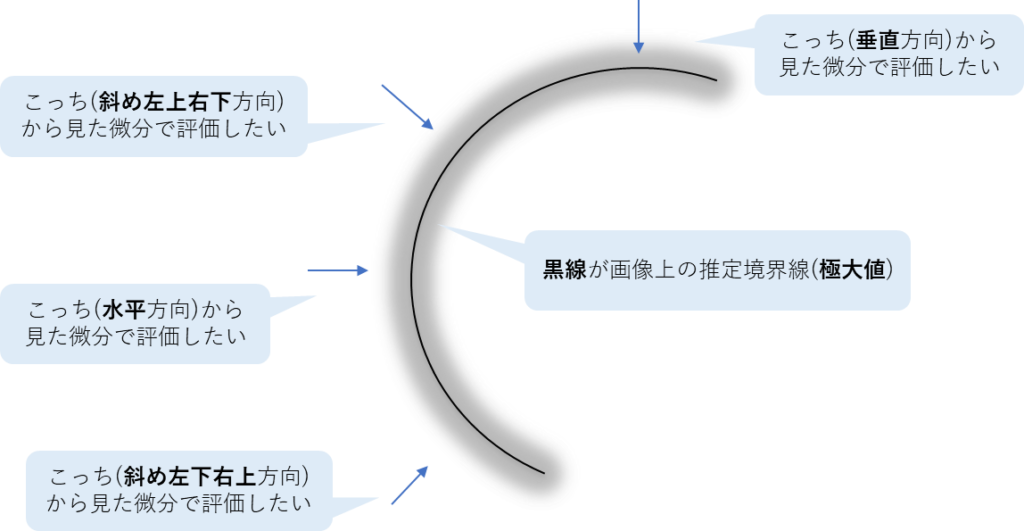
つまり、いろんな方向から見た極大値を特定しないといけない。

極大値を特定して、そこだけ残すってのも複雑な処理になりそうだし、
斜めから見るべき場所の判定とかかなり面倒そうに感じる。

が、
そこは、Sobelフィルタの途中過程の情報を使うと解決できたりする。

次のページへ