バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia3-backnumber/
はじめに
畳み込み演算の微分フィルタの話。
エッジ検出と言えば微分。
微分を離散的に考えると?
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
tanhを離散的にとらえると?

前回は、tanhで畳み込み積分をすると微分相当に結果が得られるって話だったね。

そうそう。

そして、このtanhの畳み込み積分を離散的にとらえるとどうなるかってのが今回の話。

どうなるの?

結論としてはシンプル。
引き算をすればOK!

何から何を引いたらいいんだ・・・。

tanhの関数を見るとわかるのだが、
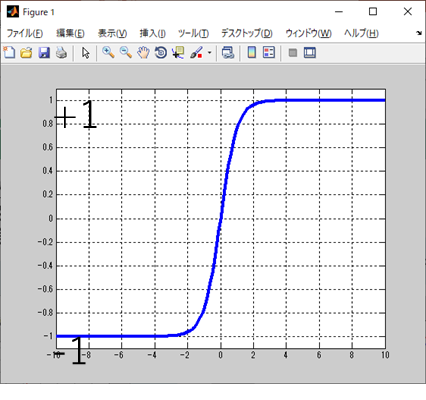

先を+1、あとを-1にしている。
つまり、以下のようなことをするだけでOK


なんだ、これだけか。
さらに値を顕著にしたい場合

さらに、畳み込みカーネルを工夫することで、変化を顕著に検出することができる。

どうするの?

少し隙間を空ける。

は?

図にするとこんな感じだな。


おー!
確かに演算結果が大き目で出てるね。
他もいろいろ

あとは、微分することでエッジ検出できることは良いのだが、
ノイズを大きく拾ってしまう可能性がある。

どうするの?

畳み込みカーネルに移動平均的なようそを付加する。

しかし、そうすると元画像の性質が消えやすくなる。

だったら、どうすんじゃい!!!

というわけで、ガウシアンカーネル的な特性を付加する。

なんか盛沢山になったような・・・。
まとめると?

で、やることをまとめるとどうなるんだ?

こんな感じかな。
以下4段階。
- 微分特性を付けてエッジ検出したい
- 微分の特性をより強くしたい
- 移動平均でノイズをちょっと除去したい
- 元画像の特徴を残すために単純移動平均じゃなくてガウシアンにしたい

つまり4つの処理をする感じ?
いや、1個目と2個目はまとめらえるのか?

一応全部まとめられる。
それを次回説明しよう。
まとめ

まとめだよ。
- tanh関数による畳み込み積分は、単なる引き算として解釈できる。
- 微分の結果を強めるには、ある程度距離がある方が良い。
- 微分するとノイズが乗りやすいので除去する策も必要。
- 元画像の特性が消えないようガウシアンにした方が良い。
バックナンバーはこちら。




コメント