MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第3章 その15【ガウシアンフィルタ①】
MATLAB,Python,Scilab,Julia比較 第3章 その16【ガウシアンフィルタ②】
MATLAB,Python,Scilab,Julia比較 第3章 その17【ガウシアンフィルタ③】
MATLAB,Python,Scilab,Julia比較 第3章 その18【ガウシアンフィルタ④】
MATLAB,Python,Scilab,Julia比較 第3章 その19【ガウシアンフィルタ⑤】
MATLAB,Python,Scilab,Julia比較 第3章 その20【ガウシアンフィルタ⑥】
を書き直したもの。
畳み込み演算のガウシアンフィルタの話になる。
これからやること
ここまでは、様々な画像処理の下準備に相当する話。
画像の読み込み、赤成分抽出、反転、書き込み、グレースケール化。
よって、これからは具体的な画像処理に該当するものを始める。
とりえあずは畳み込み演算によるガウシアンフィルタをやっていく。
畳み込み演算とは?
畳み込み演算と言うと、畳み込みニューラルネットワークが思いつくかもしれない。
やること自体は、その畳み込みと同一である。
ただし、畳み込みニューラルネットワークのように学習はせず、
特定の畳み込みカーネル(フィルタ)を固定的に使用する。
ガウシアンフィルタ?
そこで出てくるのがガウシアンフィルタ。
これは名前の通りで、ガウス分布を利用したフィルタ。
効能としてはノイズ除去になる。
ガウス分布ではなく、定数関数(常に同一の値の関数)を使用した場合は、
いわゆる移動平均と一緒になる。
いい感じに平滑化してノイズを取り除いてくれるフィルタと思って良いだろう。
説明の流れ
以下の流れで説明していく。
- 畳み込み演算
- 畳み込み積分
- 2次ガウス分布関数
- 良く使われるガウス分布カーネル
- 実際にガウシアンフィルタをやってみる
最後の「実際にガウシアンフィルタをやってみる」に関しては
この記事内ではなく、別の記事で各ツール、各言語で実施する予定。
畳み込み演算
畳み込み演算は、畳み込みニューラルネットワークの順伝播に於いての畳み込み層と同一と思って良い。
ただし、畳み込みニューラルネットワークの場合は、複数の畳み込みカーネルを用いて様々な特徴を持ったチャンネルを生成してたりするが、その点は異なる。
ここでやろうとしているのは、一つの画像に対して一つの結果を得るだけ。
要は、畳み込みニューラルネットワークでやってることと一緒ではあるけど、
それよりはるかにシンプルで簡単なことをすると思えばOK。
畳み込み演算を図解
こういうようわからんものは図解した方がよいかもしれない。
以下が畳み込み演算のイメージ。
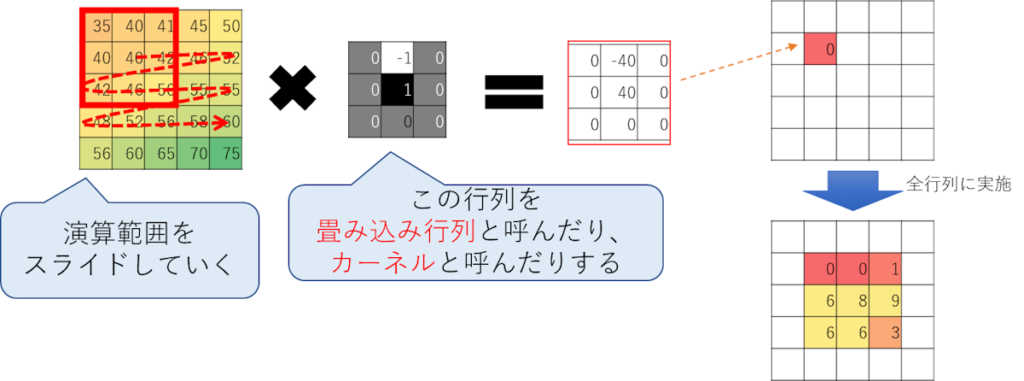
一番左が元の画像で、3×3の行列をスライドさせながらなんか計算している。
この画像の場合だと、以下の計算をしている。
\(
(35\times0)+(40\times-1)+(41\times0)+(40\times0)+(40\times1)\\+(42\times0)+(42\times0)+(46\times0)+(50\times0)=0
\)
この計算は内積と一緒である。
畳み込み演算は結果的には内積と同じ計算をしていることになる。
畳み込み積分
積分と聞くと不安になるかもしれないが、
実現手法としては掛け算と足し算の連続なので気軽にして欲しい。
どのみち、ここでは厳密な定義までは掘り下げず、雰囲気だけ察してもらうだけなので。
これにより前回やった畳み込み演算の効能が分かる。
という想定。
畳み込み積分は一言で言うと、
「関数と関数を掛けた後に定積分」
やること自体は内積とほぼ一緒。
関数を、無限次元ベクトルと解釈した上での内積となる。
\(
\begin{bmatrix}
f_1 & f_2 & \dots & f_n
\end{bmatrix}
\begin{bmatrix}
g_1 \\ g_2 \\ \vdots \\ g_n
\end{bmatrix}\Delta t
\)
畳み込み演算も内積だったので、それの元となっている畳み込み積分も内積と思えば良いだろう。
次のページへ
畳み込み積分の効能、2次ガウス分布関数を図で書く、良く使われるガウス分布カーネル、今後の方針





コメント