バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia3-backnumber/
はじめに
畳み込み演算のガウシアンフィルタの話。
今回は「良く使われるガウス分布カーネル」について。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
今回の範囲

ガウシアンフィルタ関連のやることリストを再掲
- 畳み込み演算
- 畳み込み積分
- 2次ガウス分布関数
- 良く使われるガウス分布カーネル
- 実際にガウシアンフィルタをやってみる

今回は「良く使われるガウス分布カーネル」?
なんのこっちゃ?
良く使われるガウス分布カーネル

前回、2次ガウス分布関数というのもを見せた。

中心に重みがある分布だよね。
3×3と5×5の行列が参考として算出してたね。

あれを使って、畳み込み演算をすると思ったのだけど?

まぁ、それでもOKだし、むしろそれが一番正しいのだけども、
実際のところはちょっと異なる。

つまり、別のものが使用される?

全く別ってことはないのだけど、
代表的なガウス分布カーネルってのが存在する。
以下がそれだ。
\(
\displaystyle K_{3\times3}=\frac{1}{16}
\begin{bmatrix}
1 & 2 & 1 \\
2 & 4 & 2 \\
1 & 2 & 1 \\
\end{bmatrix}=
\begin{bmatrix}
0.0625 & 0.125 & 0.0625 \\
0.125 & 0.25 & 0.125 \\
0.0625 & 0.125 & 0.0625 \\
\end{bmatrix}
\)
\(
\displaystyle K_{5\times5}=\frac{1}{256}
\begin{bmatrix}
1 & 4 & 6 & 4 & 1 \\
4 & 16 & 24 & 16 & 4\\
6 & 24 & 36 & 24 & 6\\
4 & 16 & 24 & 16 & 4\\
1 & 4 & 6 & 4 & 1 \\
\end{bmatrix}\\=
\begin{bmatrix}
0.00390625 & 0.015625 & 0.0234375 & 0.015625 & 0.00390625 \\
0.015625 & 0.0625 & 0.09375 & 0.0625 & 0.015625\\
0.0234375 & 0.09375 & 0.140625& 0.09375 & 0.0234375\\
0.015625 & 0.0625 & 0.09375 & 0.0625 & 0.015625\\
0.00390625 & 0.015625 & 0.0234375 & 0.015625 & 0.00390625 \\
\end{bmatrix}
\)
前回の2次ガウス分布を比較すると?

なんかごちゃごちゃしてるな・・・。

そして、前回の2次ガウス分布の図を再掲しよう。
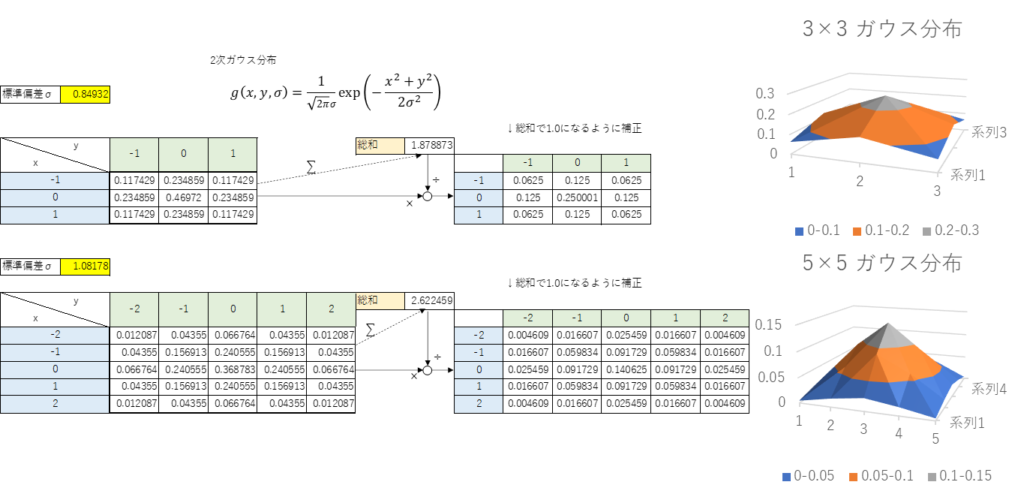

見比べるとわかるが、かなり近い値になってる。
特に3×3の方はぴったり一緒と言って良いレベルだ。

ホントだ!

というわけで、画像処理のガウシアンフィルターを実施する畳み込みカーネルは
この代表的な2つを使用することが多いってことになる。
まぁ多少誤差があっても結果に対してはさほど影響しないしね。

なるほど。
よくわからん小数を並べるよりかはスッキリした感じにはなるもんね。
期待される効能がそれほど変わらないのであれば、シンプルな方が良い気はするね。
まとめ

- 「良く使われるガウス分布カーネル」を確認。
- 前回の2次ガウス分布と大体似たような値。
- だたし、数値の表現としてはシンプル。
バックナンバーはこちら。




コメント