MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第2章 その73【多変量多項式回帰分析(関数項)②】
を書き直したもの。
正規方程式を用いた、多変量多項式回帰分析(関数項あり)について。
今回は、MATLABで演算してみる。
正規方程式、各パラメータ、推定対象の多項式再掲
多変量多項式回帰分析(関数項あり)をMATLABで実現する。
まずは恒例の正規方程式、多変量多項式回帰分析(関数項あり)で想定するパラメータの再掲。
正規方程式
\(
x=(A^TA)^{-1}A^Tb
\)
多変量多項式回帰分析(関数項あり)に於ける各パラメータ
\(
A=
\begin{bmatrix}
x_1^2 & \cos(6x_1) & y_1^2 & \exp(2y_1) &1\\
x_2^2 & \cos(6x_2) & y_2^2 & \exp(2y_2) &1\\
\vdots & \vdots & \vdots\\
x_n^2 & \cos(6x_n) & y_n^2 & \exp(2y_n) &1\\
\end{bmatrix},
\vec{x}=
\begin{bmatrix}
\alpha\\
\beta\\
\gamma\\
\delta\\
\epsilon\\
\end{bmatrix},
\vec{b}=
\begin{bmatrix}
z_1\\
z_2\\
\vdots\\
z_n
\end{bmatrix}
\)
推定対象の多項式
\(
z=4x^2-5\cos(6x)+3y^2+\exp(2y)+2
\)
MATLABコード
MATLABコードは以下になる。
n = 100;
x = rand(n, 1);
y = rand(n, 1);
z = 4*x.^2 - 5*cos(6*x) + 3*y.^2 + exp(2*y) + 2 + rand(n, 1)-0.5;
A=[x.^2 cos(6*x) y.^2 exp(2*y) ones(length(x),1)];
b=z;
X=(A'*A)^-1 *A'*b;
disp(X);
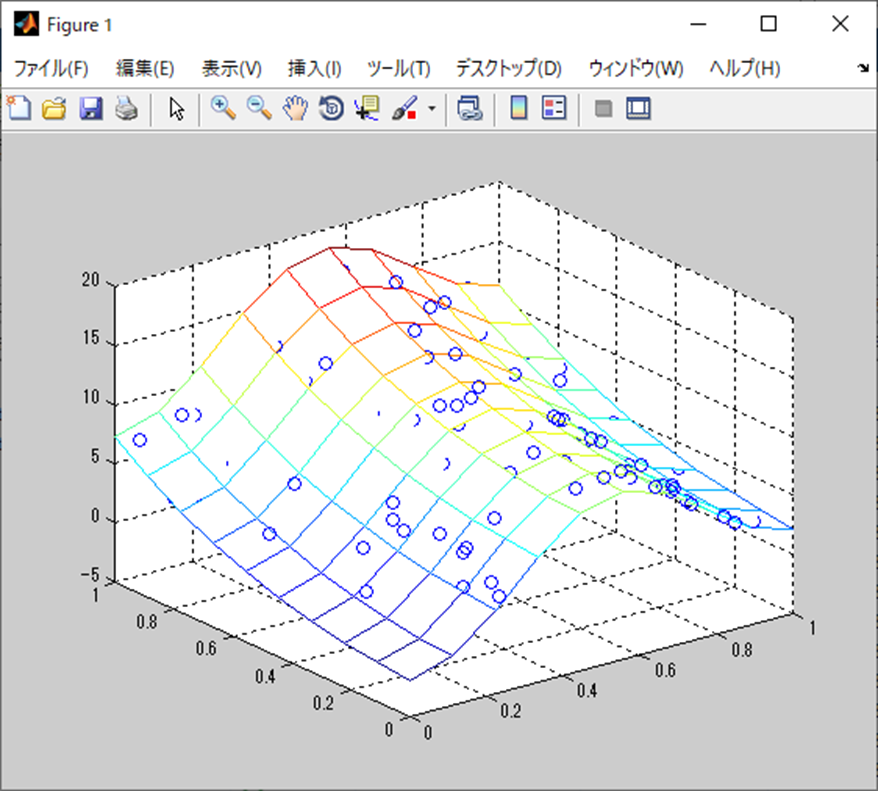
scatter3(x, y ,z);
hold on
xp=linspace(0, 1, 10);
yp=linspace(0, 1, 10);
[xpm,ypm]=meshgrid(xp,yp);
mesh( xp, yp, X(1)*xpm.^2 + X(2)*cos(6*xpm) + X(3)*ypm.^2 + X(4)*exp(2*ypm)+X(5));
hold off処理結果
処理結果は以下。
3.9746
-5.0631
3.8740
0.8655
2.2085考察
狙い通り動いてるけど、少し誤差が出てる。
サンプル点数を増やすと、当然ながら元の式と同じ係数に近付いていく。
ちなみに10000点だと以下の結果になる。
3.9843
-4.9941
2.7048
1.0476
1.9484これだと結構理想値に近い結果になっている。
コードも方もベクトル、行列の定義が変わっただけで処理手順は変化ない。
まとめ
- 正規方程式による多変量多項式回帰分析(関数項あり)をMATLABで実施。
- 誤差はあるものの目的の係数の算出はできている。
- サンプル点数を増やせば、理想値に近付く。
MATLAB、Python、Scilab、Julia比較ページはこちら





コメント