バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
MATLAB,Python,Scilab,Julia比較 第2章のまとめ。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
これまでの振り返り

というわけで、回帰分析の基礎的な部分が終わった感じだな。

な、長かった。

振り返ると、こんな感じか。
- 最小二乗法
- 普通に二乗和誤差関数で実施
- 平均、分散、共分散による算出方法実施
- 正規方程式導出
- 対称行列
- 二次形式
- 二次形式の微分
- グラム行列
- 各種回帰分析を正規方程式で実施
- 単回帰分析
- 重回帰分析
- 多項式回帰分析
- 多変量多項式回帰分析
- 多変量多項式回帰分析(関数項あり)

そうだね。

結論としては、正規方程式知ってれば問題ないってことなのか。

端的に言ってしまうとそうだね。
ただ、正規方程式も万能じゃないし、回帰分析も今回やった範囲だけでは不足な場合もある。
正規方程式じゃ無理な局面

正規方程式じゃ無理な局面って何があるの?

本シリーズの最後にやった関数項を持った多項式の関数項の内側の係数だな。

あー、確か勾配降下法を使わないといけないとか言ってたね。

それ以外にも微分項、積分項をもっても似たようなことになるだろうね。

あくまで係数と変数を掛けるだけの多項式であれば正規方程式で問題ないってことか。

そうそう。
今回以外の回帰分析

今回以外の回帰分析って何があるの?

いろいろ種類があるが、今回の延長線上のものとしては、
リッジ回帰、ラッソ回帰あたりが有名かな。

どんなもの?

基本的には、今回の回帰分析と一緒なんだけど、誤差関数に正則化項というものを付加して、過学習抑制をしている。

さっぱりわからん。

回帰分析って複雑な多項式モデルを適用できる反面、過学習しやすいんだよね。
そこに対して、正則化項というわざと精度を落とすための項を追加する。
この目的、効能からペナルティ項とも呼ばれてるようだな。

精度を落とす意味がわからん・・・。

まぁ、過学習についてのイメージを以下の画像で察してもらうしかないなー。
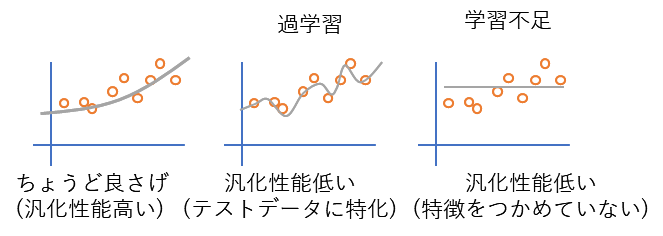

あー、なるほど。
誤差が乗ったサンプルに過剰適合しちゃうってことか。

そうそう。
そうか。太郎くんには過剰適合という言葉を使った方がわかりやすかったかもね。

詳しいことはなんもわからんけど、雰囲気はわかった。
今後について

で、このシリーズはとりあえず終了?

第2章としては終了だな。
まぁすぐに第3章が始まる可能性は高いが。

第3章はなにをやるんだ・・・。

まぁ、画像処理関連にチャレンジしてみようかと思ってる。

おー!それはなんか面白そう!

詳しくは第3章が始まった際の導入時に説明だな。
まとめ

まとめだよ。
- 第2章最終回。
- これまでの振り返り。
- 正規方程式の限界について。
- 係数と変数の積による項以外の特殊な項があると対応できない。
- 今回やった回帰分析の延長線上にあるもの。
- ラッソ回帰、リッジ回帰。
バックナンバーはこちら。




コメント