バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
正規方程式を用いた、多変量多項式回帰分析について。
今回は、MATLABで演算してみる。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
正規方程式、各パラメータ、推定対象の多項式再掲

多変量多項式回帰分析をMATLABでやるんだね。

まずは、正規方程式と多変量多項式回帰分析で想定するパラメータの再掲だ。
正規方程式
\(
x=(A^TA)^{-1}A^Tb
\)
多項式回帰分析に於ける各パラメータ
\(
A=
\begin{bmatrix}
x_1^2 & x_1y_1 & y_1^2 & y_1 &1\\
x_2^2 & x_2y_2 & y_2^2 & y_2 &1\\
\vdots & \vdots & \vdots\\
x_n^2 & x_ny_n & y_n^2 & y_n &1\\
\end{bmatrix},
\vec{x}=
\begin{bmatrix}
\alpha\\
\beta\\
\gamma\\
\delta\\
\epsilon\\
\end{bmatrix},
\vec{b}=
\begin{bmatrix}
z_1\\
z_2\\
\vdots\\
z_n
\end{bmatrix}
\)
推定対象の多項式
\(
z=4x^2-5xy+3y^2+y+2
\)
MATLABコード

MATALBコードは以下になる。
n = 100;
x = rand(1, n);
y = rand(1, n);
z = 4*x.^2 -5*x.*y + 3*y.^2 + y + 2 + rand(1, n)-0.5;
A=[x'.^2 x'.*y' y'.^2 y' ones(length(x),1)];
b=z';
X=(A'*A)^-1 *A'*b;
disp(X);
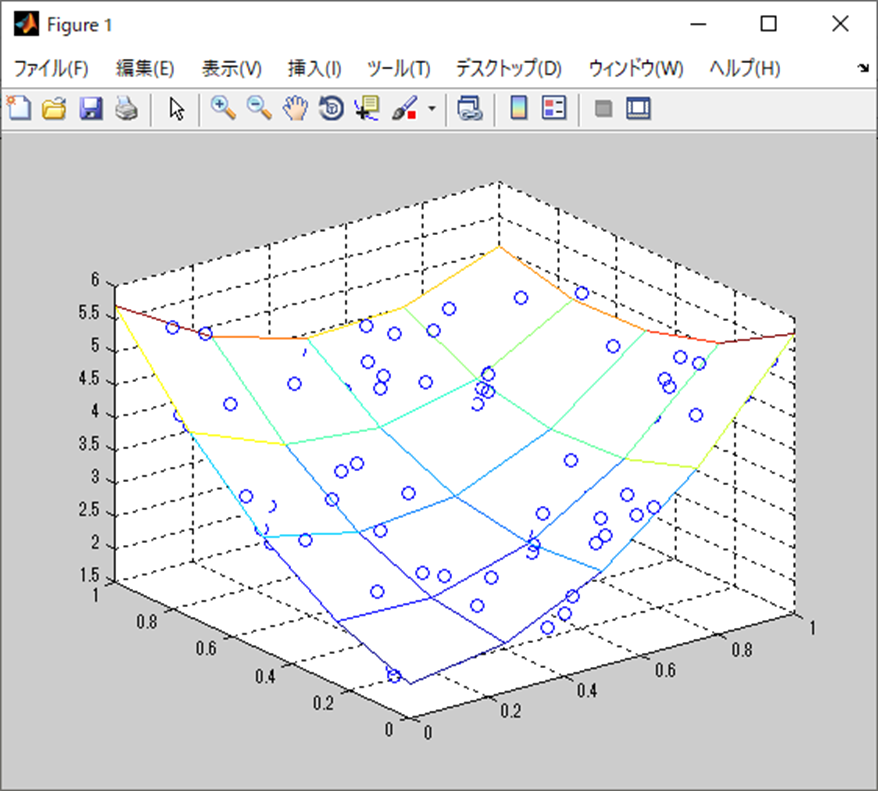
scatter3(x, y ,z);
hold on
xp=linspace(0, 1, 5);
yp=linspace(0, 1, 5);
[xpm,ypm]=meshgrid(xp,yp);
mesh( xp, yp, X(1)*xpm.^2+X(2)*xpm.*ypm+X(3)*ypm.^2+X(4)*ypm+X(5));
hold off処理結果

処理結果は以下。
3.7681
-4.4440
2.5346
1.1725
2.0029考察

まぁ、狙い通り動いてそうだけど、結構誤差が大きいようにも見えるな・・・。

式が複雑になってるからね。
サンプル点数を100から1000とかにすると一気に理想値に近付くよ。

そっか。
サンプル点数が100で、ちょっと少ないから誤差が大きく乗ってくるのか。

コードの方は、各ベクトル、行列の定義が変わっただけで、あとは一緒だね。
まとめ

まとめだよ。
- 正規方程式による多変量多項式回帰分析をMATLABで実施。
- 誤差はあるものの目的の係数の算出はできている。
- サンプル点数を増やせば、理想値に近付く。
バックナンバーはこちら。




コメント