【入門】多項式回帰分析(Python)【数値計算】

MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/

はじめに
正規方程式、各パラメータ、推定対象の多項式再掲
Pythonコード
処理結果
考察
まとめ

はじめに

の、
MATLAB,Python,Scilab,Julia比較第2章その64【多項式回帰分析③】

を書き直したもの。

正規方程式を用いた、多項式回帰分析について。
今回は、Python(NumPy)で演算してみる。

正規方程式、各パラメータ、推定対象の多項式再掲

まずは正規方程式、多項式回帰分析に於ける各パラメータ、推定対象の多項式の再掲。

正規方程式

\(
x=(A^TA)^{-1}A^Tb
\)

多項式回帰分析に於ける各パラメータ

\(
A=
\begin{bmatrix}
x_1^2 & x_1 & 1\\
x_2^2 & x_2 & 1\\
\vdots & \vdots & \vdots\\
x_n^2 & x_n & 1\\
\end{bmatrix},
\vec{x}=
\begin{bmatrix}
\alpha\\
\beta\\
\gamma
\end{bmatrix},
\vec{b}=
\begin{bmatrix}
y_1\\
y_2\\
\vdots\\
y_n
\end{bmatrix}
\)

推定対象の多項式

\(
z=4x^2-5y+2
\)

これをPython(NumPy)で解いてみる。

Pythonコード

Pythonコードは以下になる。

import numpy as np
import matplotlib.pyplot as plt

n = 100

x = np.random.rand(1, n)
y = 4*x**2-5*x+2+np.random.rand(1, n)-0.5

A=np.block([x.reshape(-1,1)**2, x.reshape(-1,1), np.ones((x.size,1))])
b=y.reshape(-1,1)
X=np.linalg.inv(A.T@A)@A.T@b
print(X)

xp = np.linspace(0, 1, 100)
plt.plot(x, y, '+b' )
plt.plot(xp, X[0]*xp**2+X[1]*xp+X[2], '-r', linewidth=3 )
plt.show()

処理結果

処理結果は以下。

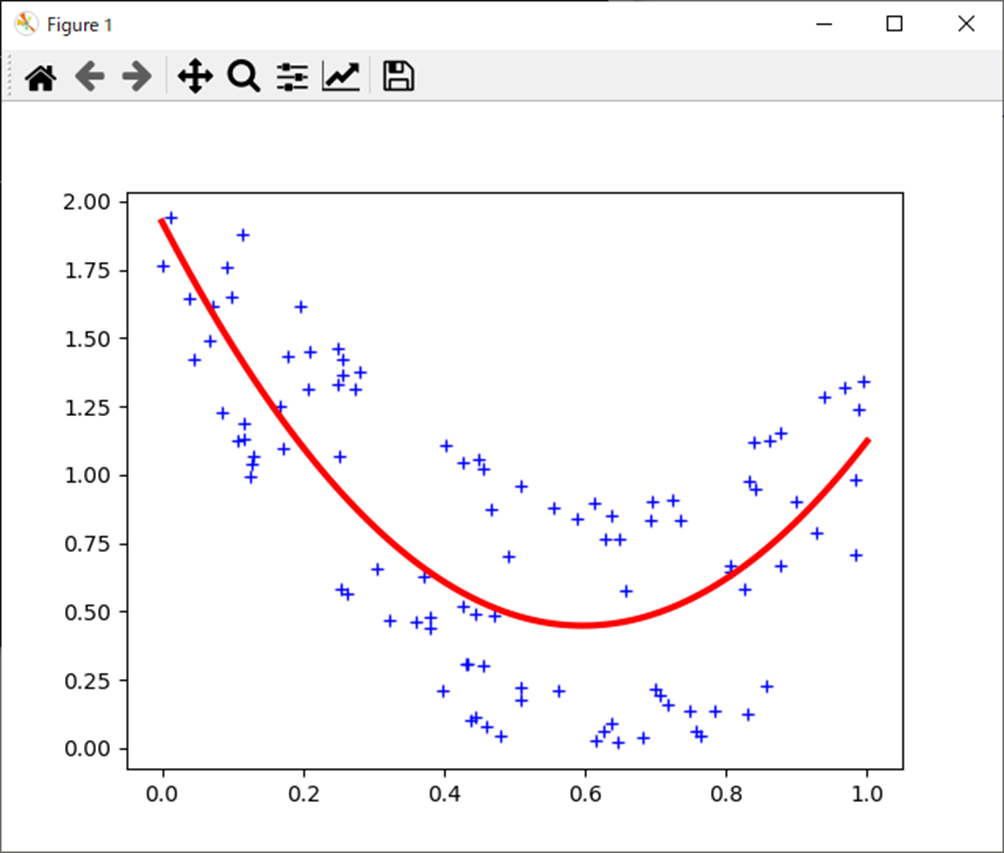
[[ 4.14882453]
 [-4.95091707]
 [ 1.92531983]]

考察

これも結果としてはOKだろう。
グラフ、係数導出も問題ない。
これも特に目立った特殊性は無いだろう。

まとめ

正規方程式による多項式回帰分析をPython(NumPy)で実施。
誤差はあるものの目的の係数の算出はできている。

バックナンバーはこちら。