MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第2章 その58【重回帰分析②】
を書き直したもの。
正規方程式を用いた、重回帰分析について。
今回は、MATLABで演算してみる。
正規方程式、各パラメータ、推定対象の多項式再掲
今回から、重回帰分析をプログラムで実現していく。
前回説明した、正規方程式と2変数の重回帰分析で想定するパラメータの再掲する。
正規方程式
\(
x=(A^TA)^{-1}A^Tb
\)
重回帰分析に於ける各パラメータ
\(
A=
\begin{bmatrix}
x_1 & y_1 & 1\\
x_2 & y_2 & 1\\
\vdots & \vdots & \vdots\\
x_n & y_n & 1\\
\end{bmatrix},
\vec{x}=
\begin{bmatrix}
\alpha\\
\beta\\
\gamma
\end{bmatrix},
\vec{b}=
\begin{bmatrix}
z_1\\
z_2\\
\vdots\\
z_n
\end{bmatrix}
\)
推定対象の多項式
\(
z=3x-2y+5
\)
MATLABコード
MATALBコードは以下になる。
n = 100;
x = rand(1, n);
y = rand(1, n);
z = 3*x-2*y+5+rand(1, n)*2-1;
A=[x',y', ones(length(x),1)];
b=z';
X=(A'*A)^-1 *A'*b;
disp(X);
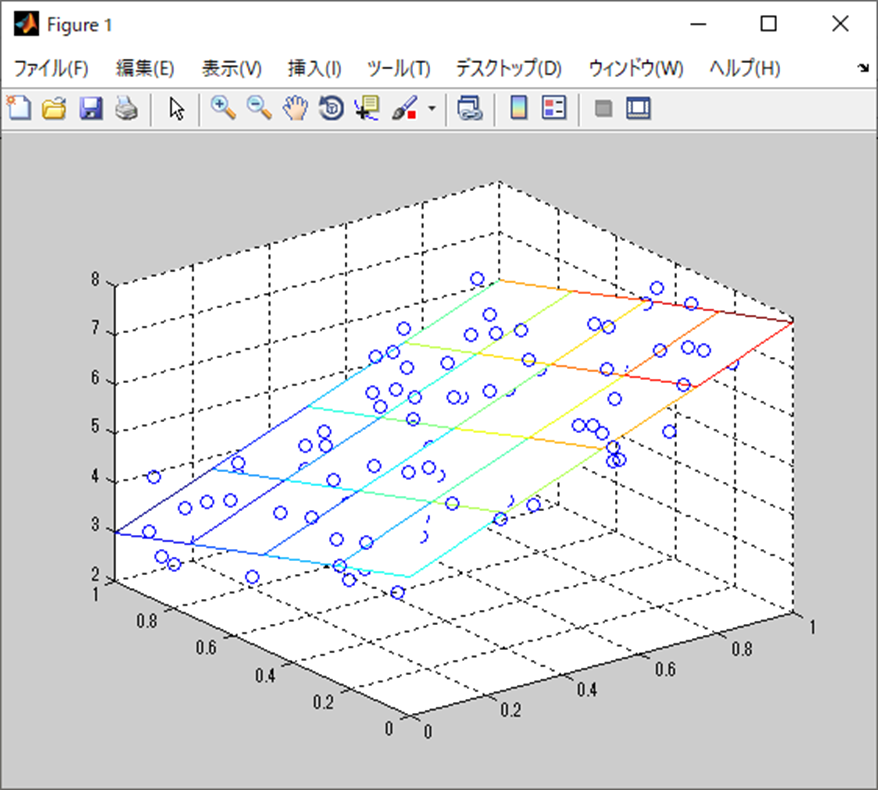
scatter3(x, y ,z);
hold on
xp=linspace(0, 1, 5);
yp=linspace(0, 1, 5);
[xpm,ypm]=meshgrid(xp,yp);
mesh( xp, yp, X(1)*xpm+X(2)*ypm+X(3));
hold off処理結果
処理結果は以下。
3.0472
-1.8768
4.8567考察
誤差は出ているが、大体\(3,-2,4\)の係数に近い感じになっている。
何度か繰り返すと分かるが、おおよそ目的の値に落ち着く結果になる。
というわけで、重回帰分析も正規方程式で実現できたと言って良いだろう。
あとはグラフ表示で
3D散布図にする場合はscatter3。
メッシュ状の平面関数を表現する場合はmesh。
を使う。
3Dグラフに関しては各ツール、各言語で結構変わることがある。
覚える必要はないが、癖の違いくらいは認識しておいた方がよいかもしれない。
まとめ
- 正規方程式による重回帰分析をMATLABで実施。
- 誤差はあるものの目的の係数の算出はできている。
- 3Dグラフの散布図はscatter3、メッシュ状の平面関数はmeshを使用して表現する。
MATLAB、Python、Scilab、Julia比較ページはこちら




コメント