バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
正規方程式を用いた、重回帰分析について。
今回は、Python(NumPy)で演算してみる。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
正規方程式、各パラメータ、推定対象の多項式再掲

太郎くん
恒例の正規方程式、各パラメータ、推定対象の多項式の再掲。
正規方程式
重回帰分析に於ける各パラメータ
推定対象の多項式

フクさん
今回は、これをPython(NumPy)を使用して解く。
Pythonコード

フクさん
Pythonコードは以下になる。
import numpy as np
import matplotlib.pyplot as plt
n = 100
x = np.random.rand(1, n)
y = np.random.rand(1, n)
z = 3*x-2*y+5+np.random.rand(1, n)*2 -1
A=np.block([x.reshape(-1,1), y.reshape(-1,1), np.ones((x.size,1))])
b=z.reshape(-1,1)
X=np.linalg.inv(A.T@A)@A.T@b
print(X)
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.scatter3D(x, y ,z)
xp=np.linspace(0, 1, 5)
yp=np.linspace(0, 1, 5)
xpm,ypm=np.meshgrid(xp,yp)
ax.plot_wireframe( xpm, ypm, X[0]*xpm+X[1]*ypm+X[2])
ax.view_init(elev=20, azim=230)
plt.show()処理結果

フクさん
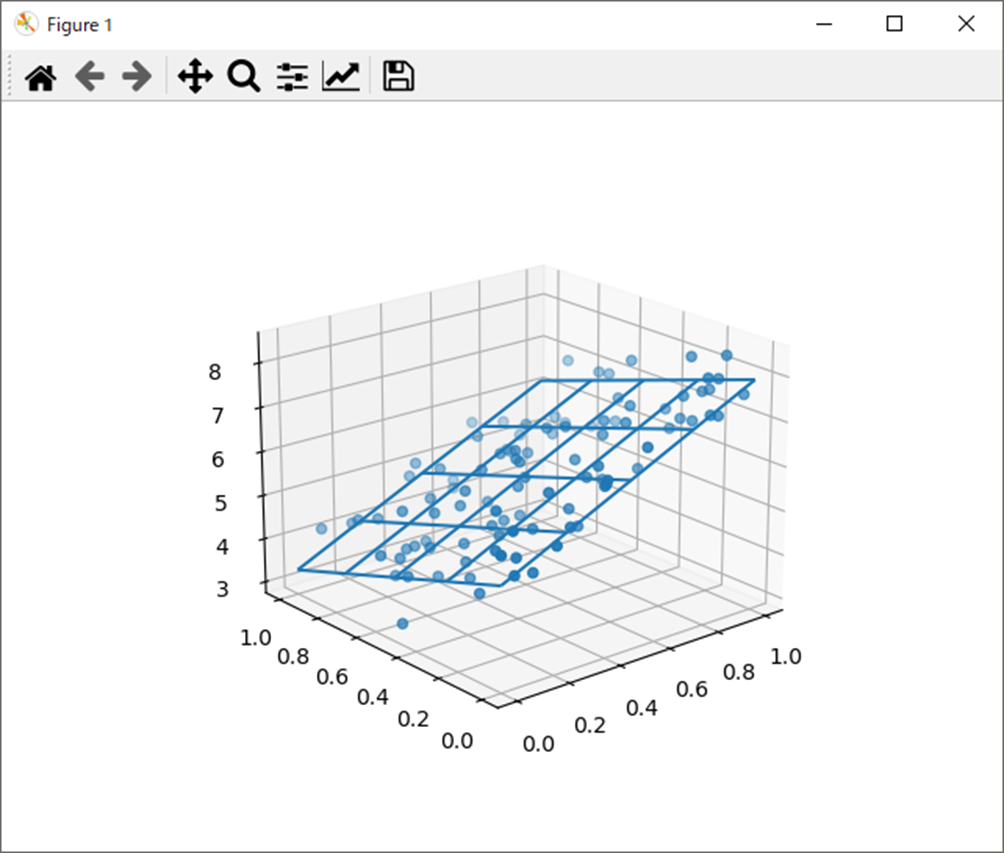
処理結果は以下。
[[ 2.85367535]
[-1.77213843]
[ 5.0744549 ]]考察

太郎くん
これも挙動としてはOKってところかな。

フクさん
これも何度か試すとを分かるが、

太郎くん
3D散布図はscatter3D、ワイヤーフレームによる平面関数はplot_wireframeで3Dグラフ表示してるね。

フクさん
3Dグラフにする際はprojection=’3d’のオプションを忘れずにね。
まとめ

フクさん
まとめだよ。
- 正規方程式による重回帰分析をPython(NumPy)で実施。
- 誤差はあるものの目的の係数の算出はできている。
- 3Dグラフの散布図はscatter3D、平面関数はplot_wireframeを使用して表現する。
- projection=’3d’のオプションを忘れずに。
バックナンバーはこちら。



コメント