MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第2章 その53【単回帰分析②】
を書き直したもの。
正規方程式を用いた、単回帰分析について。
今回は、MATLABで演算してみる。
正規方程式と各パラメータ再掲
今回から、実際にプログラミングしていく。
まずは正規方程式と単回帰分析に於ける各パラメータの再掲をしておく。
正規方程式
\(
x=(A^TA)^{-1}A^Tb
\)
単回帰分析に於ける各パラメータ
\(
A=
\begin{bmatrix}
x_1 & 1\\
x_2 & 1\\
\vdots & \vdots\\
x_n & 1\\
\end{bmatrix},
\vec{x}=
\begin{bmatrix}
\alpha\\
\beta
\end{bmatrix},
\vec{b}=
\begin{bmatrix}
y_1\\
y_2\\
\vdots\\
y_n
\end{bmatrix}
\)
MATLABコード
MATALBコードは以下になる。
x = [0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49, 2.59, 2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19, 3.23, 3.28, 3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51];
y = [10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40];
A=[x',ones(length(x),1)];
b=y';
X=(A'*A)^-1 *A'*b;
disp(X);
xp=linspace(0, 4, 400);
plot(x, y, '+', xp, X(1)*xp+X(2), '-');
ylim([10,41]);
xlim([0,4]);
処理結果
処理結果は以下。
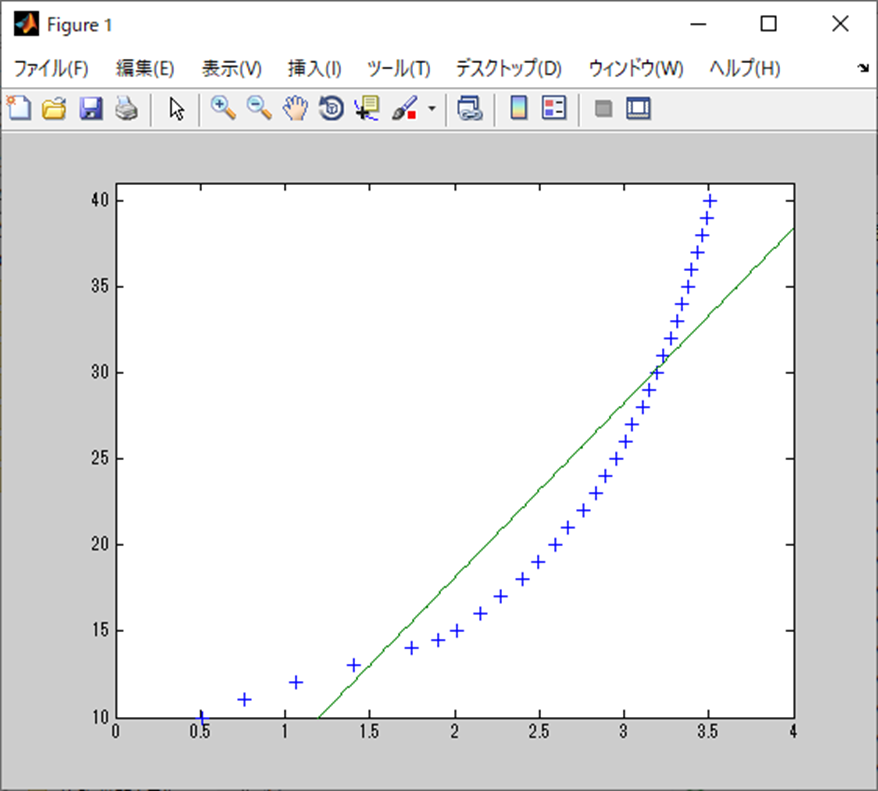
10.1330
-2.1617考察
以前の最小二乗法で使用したものと同じサンプリングで処理しているため、
その時に導出した係数と同じものが算出されている。
よって、計算としては合っていると思って良いだろう。
処理としては、数式で定義したものをそのまま実施している。
これはベクトル、行列の演算ができる環境ならではの効能。
まとめ
- 正規方程式による単回帰分析をMATLABで実施。
- 以前の最小二乗法と同じ結果が得られた。
- 数式で定義した通りの演算をするのみ。
MATLAB、Python、Scilab、Julia比較ページはこちら





コメント