バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
正規方程式を用いた、単回帰分析について。
今回は、Juliaで演算してみる。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
正規方程式と各パラメータ再掲

まずは正規方程式と単回帰分析に於ける各パラメータの再掲。
正規方程式
\(
x=(A^TA)^{-1}A^Tb
\)
単回帰分析に於ける各パラメータ
\(
A=
\begin{bmatrix}
x_1 & 1\\
x_2 & 1\\
\vdots & \vdots\\
x_n & 1\\
\end{bmatrix},
\vec{x}=
\begin{bmatrix}
\alpha\\
\beta
\end{bmatrix},
\vec{b}=
\begin{bmatrix}
y_1\\
y_2\\
\vdots\\
y_n
\end{bmatrix}
\)

今回は、これをJuliaを使用して解いてみる。
Juliaコード

Juliaコードは以下になる。
using PyPlot
x = [0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49,
2.59, 2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19,
3.23, 3.28, 3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51]
y = [10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23,
24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40]
A=[x ones(length(x),1)];
b=y;
X=(A'*A)^-1 *A'*b;
print(X);
xp=range(0, 4, length=400);
plot(x, y, "+");
plot(xp, X[1].*xp.+X[2], "-");
ylim([10,41]);
xlim([0,4]);処理結果

処理結果は以下。
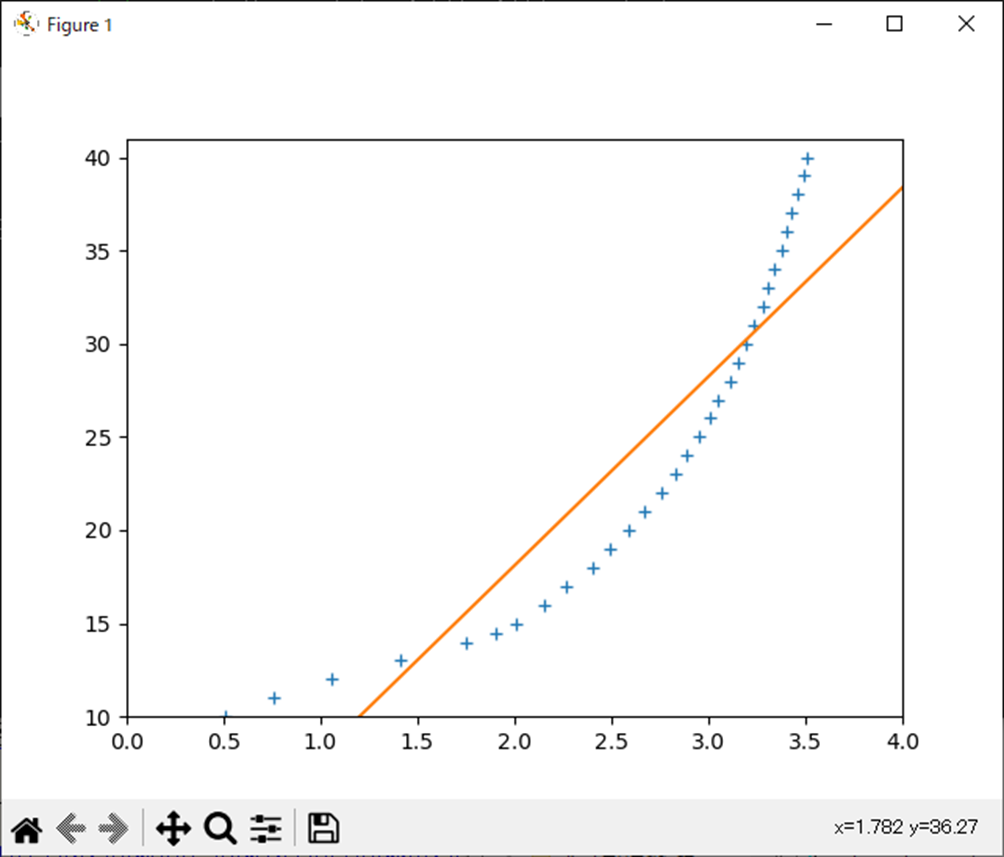
[10.133033511230932, -2.161664366928431]考察

これもMATLABと結果は一緒かな。
表示精度が大きく違うけど。

そうだね。
MATLABも表示精度を上げれば、同じ値になるな。

あとは、演算部分もMATLABと一緒かな。

違いはplot時のX[1].*xp.+X[2]で「.」によるベクトル化演算子を使用する点だな。

あー、Juliaはこれがあるんだった・・・。

まぁこれによって、JITコンパイル時の効率的なコードを生成のヒントにしているようだから、
処理速度という面では重要な演算子だな。

Juliaの良さを引き出すための必要なものだね。
まとめ

まとめだよ。
- 正規方程式による単回帰分析をJuliaで実施。
- MATLABと同じ結果が得られた。
- 演算部分はMTALABと同一。
- ベクトル化演算子であるdot演算子を利用する局面はある。
バックナンバーはこちら。




コメント