MATLAB、Scilab、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第2章 その36【対称行列と二次形式⑧】
を書き直したもの。
正規方程式を導出するための対称行列と二次形式の話。
今回は二次形式の多項式表現と行列表現の計算をJuliaで実施する。
ロードマップ【再掲】
ロードマップと今回使用する数式を再掲。

\(
x^TA\circ x^T
\begin{bmatrix}
1\\
\vdots\\
1
\end{bmatrix}
\)
計算する二次形式の数式
\(
3x^2+2y^2+5xy
\)
今回は、Juliaで実施する。
Juliaコード
Juliaコードは以下になる。
using PyPlot
function meshgrid(xin,yin)
nx=length(xin)
ny=length(yin)
xout=zeros(ny,nx)
yout=zeros(ny,nx)
for jx=1:nx
for ix=1:ny
xout[ix,jx]=xin[jx]
yout[ix,jx]=yin[ix]
end
end
return (x=xout, y=yout)
end
a=3;
b=2;
c=5;
A=[a c/2; c/2 b];
N=6;
ax=range(0,10,length=N);
ay=range(0,10,length=N);
x,y=meshgrid(ax,ay);
fig, (ax1, ax2) = plt.subplots(2, 1,
figsize=(8, 8),
subplot_kw=Dict("projection" => "3d"))
polyY=a.*x.^2+b.*y.^2+c.*x.*y;
ax1.plot_wireframe(x, y, polyY, rstride=1, cstride=1);
X=[x[:]';y[:]'];
Y=X'*A.*X'*ones(2,1);
matY=reshape(Y,N,N);
ax2.plot_wireframe(x, y, matY);
plt.tight_layout()
plt.show()
polyY
matY実行結果
実行結果は以下になる。
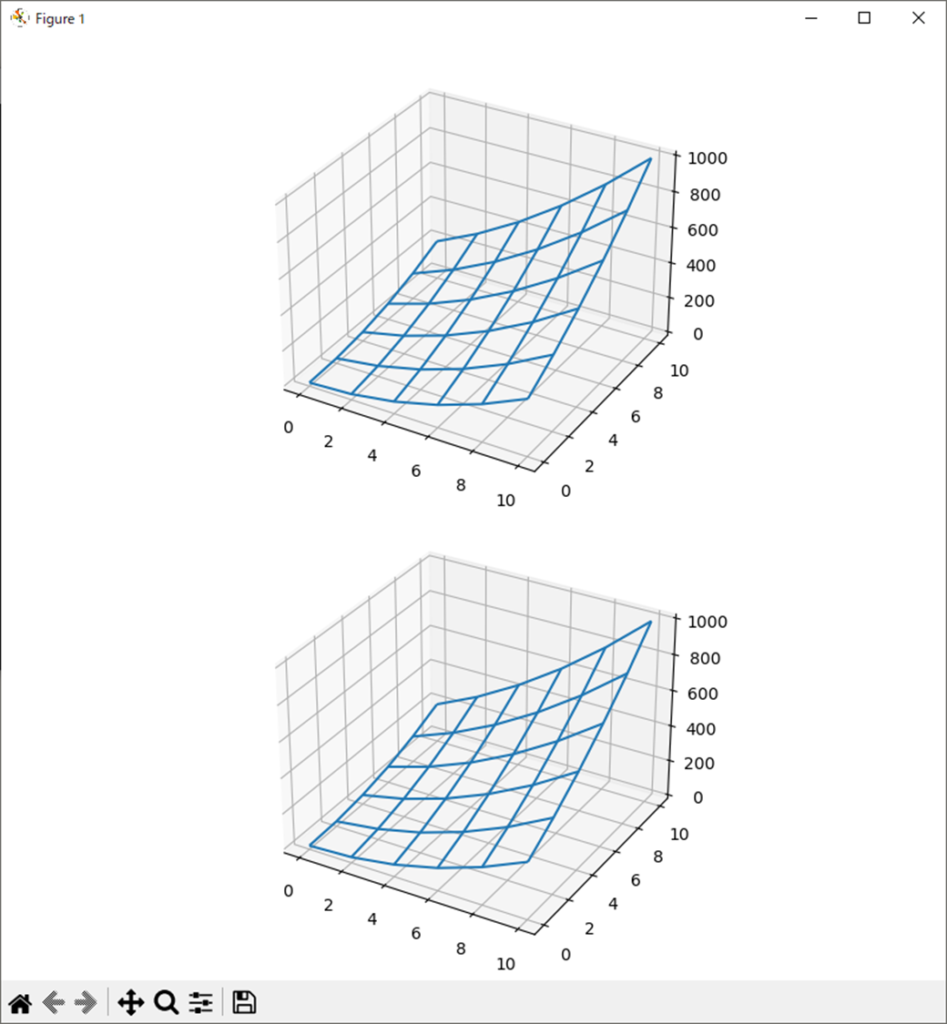
polyY
6×6 Matrix{Float64}:
0.0 12.0 48.0 108.0 192.0 300.0
8.0 40.0 96.0 176.0 280.0 408.0
32.0 84.0 160.0 260.0 384.0 532.0
72.0 144.0 240.0 360.0 504.0 672.0
128.0 220.0 336.0 476.0 640.0 828.0
200.0 312.0 448.0 608.0 792.0 1000.0
matY
6×6 Matrix{Float64}:
0.0 12.0 48.0 108.0 192.0 300.0
8.0 40.0 96.0 176.0 280.0 408.0
32.0 84.0 160.0 260.0 384.0 532.0
72.0 144.0 240.0 360.0 504.0 672.0
128.0 220.0 336.0 476.0 640.0 828.0
200.0 312.0 448.0 608.0 792.0 1000.0考察
二次形式の多項式表現と、行列表現に差異がないことは確認できた。
コードとしては、MATLABとPythonを混ぜたような感じになった。
演算部分は、MATLABと同じだが、
グラフの描画がPyPlotを使ってる影響でPythonに近い。
PyPlot自体はpythonで使用したmatplotlibのラッパーだから、そうなるのだろう。
あと、meshgridを自作している。
類似関数が無いか探したのだけど、見つからず、結果自作した。
もしかしたらmeshgridを使うのとは別の平面座標生成方法がJuliaのセオリーとしてあるのかもしれないが、
ちょっと見つけられなかったな。
まとめ
- 二次形式の多項式表現と行列表現の計算をJuliaで実施。
- 3Dグラフを表示する際は、”projection” => “3d”が必要。
- meshgridが無いので自作した。
MATLAB、Python、Scilab、Julia比較ページはこちら





コメント